John-Nirenberg inequalities
Functions in Hardy spaces and in 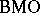 .
.
Let 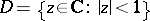 be the unit disc and let, for
be the unit disc and let, for 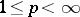 ,
, 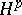 denote the space of holomorphic functions on
denote the space of holomorphic functions on 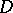 (cf. also Analytic function) for which the supremum
(cf. also Analytic function) for which the supremum
 |
is finite. If a function  belongs to
belongs to  ,
, 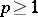 , then there exists a function
, then there exists a function 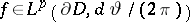 such that
such that
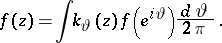 |
Here, the function
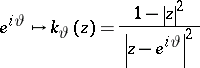 |
is the probability density (cf. also Density of a probability distribution) of a Brownian motion starting at 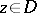 and exiting
and exiting 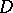 at
at 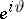 . It is the Poisson kernel (cf. also Poisson integral) for the unit disc. A function
. It is the Poisson kernel (cf. also Poisson integral) for the unit disc. A function 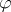 , defined on
, defined on 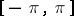 , belongs to
, belongs to 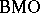 if there exists a constant
if there exists a constant  such that
such that 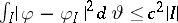 , for all intervals
, for all intervals 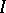 (cf. also
(cf. also 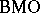 -space). Here,
-space). Here, 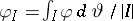 and
and 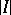 denotes the Lebesgue measure of the interval
denotes the Lebesgue measure of the interval 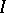 . Let
. Let 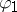 and
and 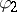 be bounded real-valued functions defined on the boundary
be bounded real-valued functions defined on the boundary 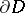 of
of 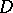 , and let
, and let 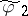 be the boundary function of the harmonic conjugate function of the harmonic extension to
be the boundary function of the harmonic conjugate function of the harmonic extension to 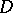 of
of 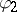 (cf. also Conjugate harmonic functions), so that
(cf. also Conjugate harmonic functions), so that 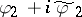 is the boundary function of a function which is holomorphic on
is the boundary function of a function which is holomorphic on 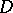 . Then the function
. Then the function 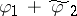 belongs to
belongs to 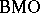 : see [a4], p. 200, or [a9], p. 295. The function
: see [a4], p. 200, or [a9], p. 295. The function
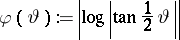 |
belongs to 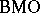 , but is not bounded; see [a6], Chap. VI. Composition with the biholomorphic mapping
, but is not bounded; see [a6], Chap. VI. Composition with the biholomorphic mapping
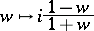 |
turns 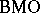 -functions of the line into
-functions of the line into 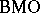 -functions of the circle; see [a6], p. 226.
-functions of the circle; see [a6], p. 226.
Martingales in Hardy spaces and in 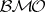 .
.
Let 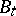 ,
, 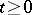 , be Brownian motion starting at
, be Brownian motion starting at  and let
and let 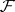 be the filtration generated by Brownian motion (cf. also Stochastic processes, filtering of). Notice that
be the filtration generated by Brownian motion (cf. also Stochastic processes, filtering of). Notice that 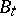 ,
, 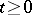 , is a continuous Gaussian process with covariance
, is a continuous Gaussian process with covariance 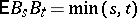 . Define, for
. Define, for 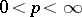 , the space of local martingales
, the space of local martingales 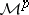 by
by
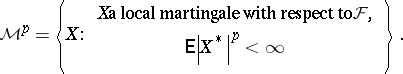 |
Here, 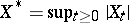 . Since the martingales are
. Since the martingales are 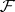 -martingales, they can be written in the form of an Itô integral:
-martingales, they can be written in the form of an Itô integral:
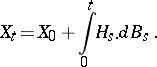 |
Here, 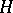 is a predictable random process. Let
is a predictable random process. Let 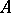 be a
be a 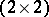 -matrix, and define the
-matrix, and define the 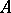 -transform of
-transform of 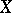 by
by 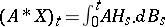 . Then the martingale
. Then the martingale 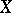 belongs to
belongs to 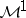 if and only all transformed martingales
if and only all transformed martingales 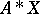 have the property that
have the property that
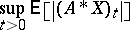 |
is finite; this is Janson's theorem [a8]. A martingale 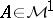 is called an atom if there exists a stopping time
is called an atom if there exists a stopping time 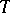 such that
such that
i) 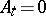 if
if 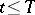 ; and
; and
ii)
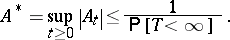 |
Since for atoms 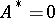 on the event
on the event 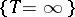 , it follows that
, it follows that 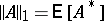 . Moreover, every
. Moreover, every 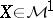 can be viewed as a limit of the form
can be viewed as a limit of the form
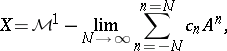 |
where every 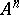 is an atom and where
is an atom and where 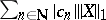 . A local martingale
. A local martingale 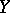 is said to have to bounded mean oscillation (notation
is said to have to bounded mean oscillation (notation 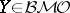 ) if there exists a constant
) if there exists a constant  such that
such that
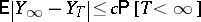 |
for all  -stopping times
-stopping times 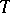 . The infimum of the constants
. The infimum of the constants  is the
is the 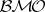 -norm of
-norm of 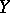 . It is denoted by
. It is denoted by 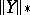 . The above inequality is equivalent to
. The above inequality is equivalent to
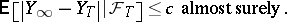 |
Let 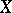 be a non-negative martingale. Put
be a non-negative martingale. Put 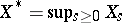 . Then
. Then 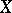 belongs to
belongs to 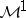 if and only if
if and only if 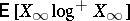 is finite. More precisely, the following inequalities are valid:
is finite. More precisely, the following inequalities are valid:
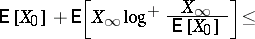 |
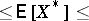 |
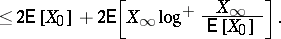 |
For details, see e.g. [a4], p. 149. Let 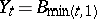 . Then
. Then 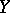 is an unbounded martingale in
is an unbounded martingale in 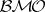 . Two main versions of the John–Nirenberg inequalities are as follows.
. Two main versions of the John–Nirenberg inequalities are as follows.
Analytic version of the John–Nirenberg inequality.
There are constants 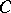 ,
, 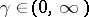 , such that, for any function
, such that, for any function 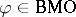 for which
for which 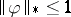 , the inequality
, the inequality
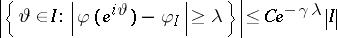 |
is valid for all intervals 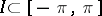 .
.
Probabilistic version of the John–Nirenberg inequality.
There exists a constant 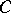 such that for any martingale
such that for any martingale 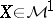 for which
for which 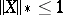 , the inequality
, the inequality 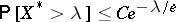 is valid. For the same constant
is valid. For the same constant 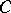 , the inequality
, the inequality
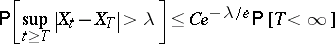 |
is valid for all 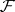 -stopping times
-stopping times 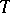 and for all
and for all 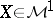 for which
for which 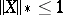 .
.
As a consequence, for 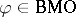 integrals of the form
integrals of the form 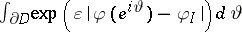 are finite for
are finite for 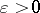 sufficiently small.
sufficiently small.
Duality between 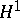 and
and 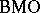 .
.
The John–Nirenberg inequalities can be employed to prove the duality between the space of holomorphic functions 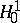 and
and 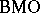 and between
and between 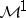 and
and 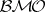 .
.
Duality between 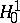 and
and 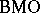 (analytic version).
(analytic version).
The duality between 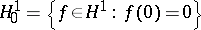 and
and 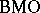 is given by
is given by
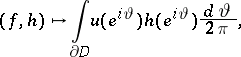 |
where 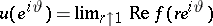 (
(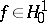 ,
, 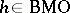 ).
).
Duality between 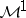 and
and 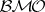 (probabilistic version).
(probabilistic version).
Let 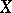 be a martingale in
be a martingale in 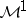 and let
and let 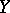 be a martingale in
be a martingale in 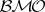 . The duality between these martingales is given by
. The duality between these martingales is given by 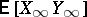 . Here,
. Here, 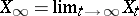 and
and 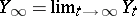 .
.
There exists a more or less canonical way to identify holomorphic functions in 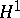 and certain continuous martingales in
and certain continuous martingales in 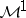 . Moreover, the same is true for functions of bounded mean oscillation (functions in
. Moreover, the same is true for functions of bounded mean oscillation (functions in 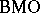 ) and certain continuous martingales in
) and certain continuous martingales in 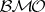 . Consequently, the duality between
. Consequently, the duality between 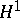 and
and 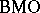 can also be extended to a duality between
can also be extended to a duality between 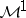 -martingales and
-martingales and 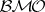 -martingales.
-martingales.
The relationship between 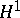 (respectively,
(respectively, 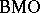 ) and a closed subspace of
) and a closed subspace of 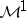 (respectively,
(respectively, 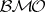 ) is determined via the following equalities. For
) is determined via the following equalities. For 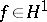 one writes
one writes 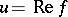 and
and 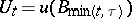 , and for
, and for 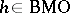 one writes
one writes 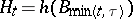 , where, as above,
, where, as above, 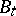 is two-dimensional Brownian motion starting at
is two-dimensional Brownian motion starting at  , and where
, and where 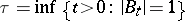 . Then the martingale
. Then the martingale 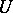 belongs to
belongs to 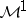 , and
, and 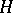 is a member of
is a member of 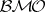 . The fact that
. The fact that 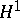 can be considered as a closed subspace of
can be considered as a closed subspace of 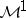 is a consequence of the following
is a consequence of the following
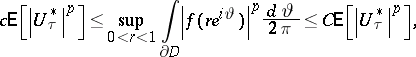 |
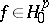 ,
, 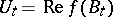 ,
, 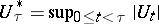 .
.
An important equality in the proof of these dualities is the following result: Let 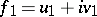 and
and 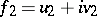 be functions in
be functions in 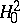 . Then
. Then
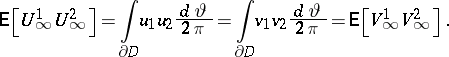 |
Here, 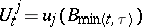 ,
, 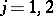 . A similar convention is used for
. A similar convention is used for 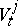 ,
, 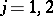 . In the first (and in the final) equality, the distribution of
. In the first (and in the final) equality, the distribution of  is used:
is used: 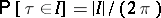 . The other equalities depend on the fact that a process like
. The other equalities depend on the fact that a process like 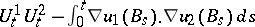 is a martingale, which follows from Itô calculus in conjunction with the harmonicity of the functions
is a martingale, which follows from Itô calculus in conjunction with the harmonicity of the functions 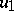 and
and 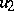 . Next, let
. Next, let 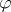 be a function in
be a function in 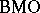 . Denote by
. Denote by 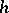 the harmonic extension of
the harmonic extension of 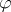 to
to 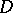 . Put
. Put 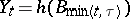 . Then
. Then 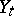 is a continuous martingale. Let
is a continuous martingale. Let 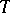 be any stopping time. From the Markov property it follows that
be any stopping time. From the Markov property it follows that 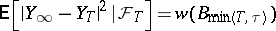 , where
, where
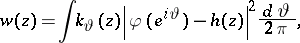 |
with
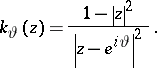 |
As above, the Poisson kernel for the unit disc 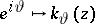 can be viewed as the probability density of a Brownian motion starting at
can be viewed as the probability density of a Brownian motion starting at 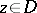 and exiting
and exiting 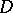 at
at 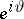 . Since the inequality
. Since the inequality 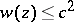 is equivalent to the inequality
is equivalent to the inequality
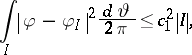 |
for some constant 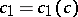 , it follows that
, it follows that 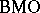 can be considered as a closed subspace of
can be considered as a closed subspace of 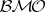 : see [a6], Corol. 2.4; p. 234.
: see [a6], Corol. 2.4; p. 234.
The analytic John–Nirenberg inequality can be viewed as a consequence of a result due to A.P. Calderón and A. Zygmund. Let  be function in
be function in 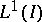 (
(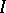 is some interval). Suppose
is some interval). Suppose 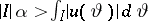 . Then there exists a pairwise disjoint sequence
. Then there exists a pairwise disjoint sequence 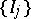 of open subintervals of
of open subintervals of 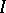 such that
such that 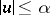 almost everywhere on
almost everywhere on 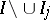 ,
,
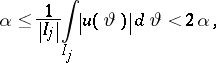 |
and
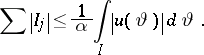 |
In [a1], [a6], [a7] and [a10], extensions of the above can be found. In particular, some of the concepts can be extended to other domains in  (see [a6]), in
(see [a6]), in  and in more general Riemannian manifolds ([a1], [a2], [a7], [a10]). For a relationship with Carleson measures, see [a6], Chap. 6. A measure
and in more general Riemannian manifolds ([a1], [a2], [a7], [a10]). For a relationship with Carleson measures, see [a6], Chap. 6. A measure 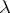 on
on 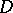 is called a Carleson measure if
is called a Carleson measure if 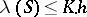 for some constant
for some constant 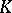 and for all circle sectors
and for all circle sectors 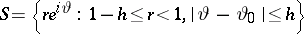 . A function
. A function 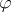 belongs to
belongs to 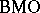 if and only if
if and only if
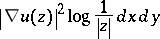 |
is a Carleson measure. Here,  is the harmonic extension of
is the harmonic extension of 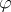 . For some other phenomena and related inequalities, see e.g. [a3], [a10], and [a11].
. For some other phenomena and related inequalities, see e.g. [a3], [a10], and [a11].
References
| [a1] | M. Biroli, U. Mosco, "Sobolev inequalities on homogeneous spaces: Potential theory and degenerate partial differential operators (Parma)" Potential Anal. , 4 (1995) pp. 311–324 |
| [a2] | S.Y.A. Chang, R. Fefferman, "A continuous version of duality of 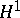 with with 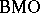 on the bidisc" Ann. of Math. (2) , 112 (1980) pp. 179–201 on the bidisc" Ann. of Math. (2) , 112 (1980) pp. 179–201 |
| [a3] | L. Chevalier, "Quelles sont les fonctions qui opèrent de 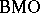 dans dans 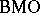 ou de ou de 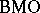 dans dans 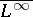 " Bull. London Math. Soc. , 27 : 6 (1995) pp. 590–594 " Bull. London Math. Soc. , 27 : 6 (1995) pp. 590–594 |
| [a4] | R. Durrett, "Brownian motion and martingales in analysis" , Wadsworth (1984) (Contains Mathematica analysis and stochastic processes) MR0750829 Zbl 0554.60075 |
| [a5] | J.B. Garnett, "Two constructions in 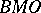 " G. Weiss (ed.) S. Wainger (ed.) , Harmonic analysis in Euclidean spaces , Proc. Symp. Pure Math. , XXXV:1 , Amer. Math. Soc. (1979) pp. 295–301 " G. Weiss (ed.) S. Wainger (ed.) , Harmonic analysis in Euclidean spaces , Proc. Symp. Pure Math. , XXXV:1 , Amer. Math. Soc. (1979) pp. 295–301 |
| [a6] | J. Garnett, "Bounded analytic functions" , Acad. Press (1981) MR0628971 Zbl 0469.30024 |
| [a7] | R. Hurri-Syrjanen, "The John–Nirenberg inequality and a Sobolev inequality in general domains" J. Math. Anal. Appl. , 175 : 2 (1993) pp. 579–587 |
| [a8] | S. Janson, "Characterization of 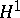 by singular integral transformations on martingales and by singular integral transformations on martingales and 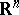 " Math. Scand. , 41 (1977) pp. 140–152 " Math. Scand. , 41 (1977) pp. 140–152 |
| [a9] | P. Koosis, "Introduction to 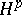 -spaces: with an appendix on Wolff's proof of the corona theorem" , London Math. Soc. Lecture Notes , 40 , London Math. Soc. (1980) -spaces: with an appendix on Wolff's proof of the corona theorem" , London Math. Soc. Lecture Notes , 40 , London Math. Soc. (1980) |
| [a10] | Jia-Yu Li, "On the Harnack inequality for harmonic functions on complete Riemannian manifolds" Chinese Ann. Math. Ser. B , 14 : 1 (1993) pp. 1–12 |
| [a11] | F.J. Martin–Reyes, A. de la Torre, "One-sided 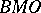 spaces" J. London Math. Soc. (2) , 49 : 3 (1994) pp. 529–542 spaces" J. London Math. Soc. (2) , 49 : 3 (1994) pp. 529–542 |
| [a12] | G. Weiss, "Weak-type inequalities for 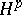 and and 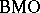 " G. Weiss (ed.) S. Wainger (ed.) , Harmonic Analysis in Euclidean Spaces , Proc. Symp. Pure Math. , XXXV:1 , Amer. Math. Soc. (1979) pp. 295–301 " G. Weiss (ed.) S. Wainger (ed.) , Harmonic Analysis in Euclidean Spaces , Proc. Symp. Pure Math. , XXXV:1 , Amer. Math. Soc. (1979) pp. 295–301 |
John-Nirenberg inequalities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=John-Nirenberg_inequalities&oldid=50287