Wilf quadrature formulas
Wilf formulas
Quadrature formulas (cf. Quadrature formula) constructed from a Hilbert space setting.
Let 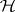 be a Hilbert space of continuous functions such that
be a Hilbert space of continuous functions such that 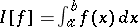 and
and 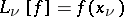 are continuous functionals; let
are continuous functionals; let 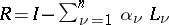 for
for 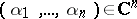 . Riesz's representation theorem guarantees the existence of an
. Riesz's representation theorem guarantees the existence of an 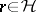 such that
such that 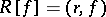 . By the Schwarz inequality (cf. Bunyakovskii inequality) one has
. By the Schwarz inequality (cf. Bunyakovskii inequality) one has 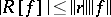 in the Hilbert space norm. The formula is called optimal in
in the Hilbert space norm. The formula is called optimal in 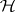 if
if  and
and  are chosen such as to minimize
are chosen such as to minimize  . If
. If 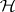 has a continuously differentiable reproducing kernel
has a continuously differentiable reproducing kernel 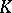 , then such optimal formulas necessarily satisfy [a1]
, then such optimal formulas necessarily satisfy [a1]
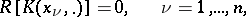 |
and
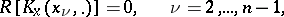 |
and 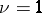 (
( ) if
) if 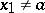 (
(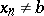 ). Here,
). Here, 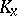 denotes the derivative with respect to the first variable. Formulas which satisfy these conditions are called Wilf formulas.
denotes the derivative with respect to the first variable. Formulas which satisfy these conditions are called Wilf formulas.
The problem of minimizing  can also be considered for fixed nodes
can also be considered for fixed nodes  . These formulas are characterized by integrating the unique element of least norm in
. These formulas are characterized by integrating the unique element of least norm in 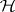 which interpolates
which interpolates  at the nodes
at the nodes 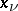 . An analogous statement holds for Hermite quadrature formulas of the type
. An analogous statement holds for Hermite quadrature formulas of the type 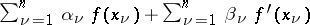 . The Wilf formula for free nodes is the Wilf formula for those fixed nodes for which
. The Wilf formula for free nodes is the Wilf formula for those fixed nodes for which 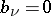 [a1], [a3].
[a1], [a3].
The original construction of H.S. Wilf [a4] was for the Hardy space (cf. also Hardy spaces) of functions which are analytic inside the open disc with radius 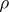 , with inner product
, with inner product
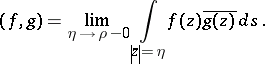 |
In the Hardy space the necessary conditions have a unique solution. The nodes are in 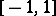 , the weights are positive and
, the weights are positive and 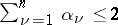 . For fixed
. For fixed  and
and 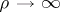 these formulas converge to the Gaussian formulas (cf. also Gauss quadrature formula) [a1]. They can be constructed from a suitable rational interpolant [a1], [a3].
these formulas converge to the Gaussian formulas (cf. also Gauss quadrature formula) [a1]. They can be constructed from a suitable rational interpolant [a1], [a3].
For fixed nodes  , the inner product
, the inner product
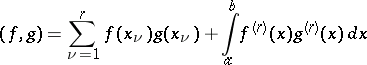 |
leads to the Sard quadrature formula, which is optimal in the class of functions 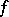 with
with 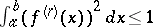 [a1], [a2], [a3] (see Optimal quadrature; Best quadrature formula). The Sard formula results from integrating the natural spline function of order
[a1], [a2], [a3] (see Optimal quadrature; Best quadrature formula). The Sard formula results from integrating the natural spline function of order  which interpolates
which interpolates  at the nodes
at the nodes  [a1].
[a1].
References
| [a1] | H. Braß, "Quadraturverfahren" , Vandenhoeck&Ruprecht (1977) |
| [a2] | P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1984) (Edition: Second) |
| [a3] | H. Engels, "Numerical quadrature and cubature" , Acad. Press (1980) |
| [a4] | H.S. Wilf, "Exactness conditions in numerical quadrature" Numer. Math. , 6 (1964) pp. 315–319 |
Wilf quadrature formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wilf_quadrature_formulas&oldid=50278