Dirichlet algebra

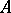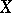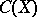Let be a uniform algebra on and the algebra of all continuous functions on 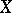(cf. also Algebra of functions). The algebra 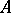is called a Dirichlet algebra if 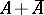is uniformly dense in 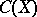. Dirichlet algebras were introduced by A.M. Gleason [a4].

Let 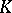be a compact subset of the complex plane. Let 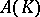consist of those functions which are analytic on the interior of 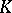and let 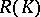be the uniform closure in 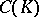of the functions analytic on a neighbourhood of 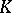. T. Gamelin and J. Garnett [a3] determined exactly when 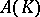or 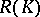is a Dirichlet algebra on 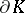. The disc algebra 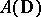is the algebra of all functions which are analytic in the open unit disc 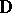and continuous in the closed unit disc 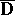. The algebra 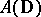is a typical example of a Dirichlet algebra on the unit circle 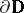. For 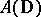, the measure

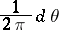is the representing measure for the origin, that is,

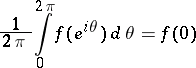for 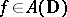. The origin gives a complex homomorphism fo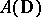r . For 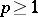, the Hardy space 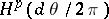is defined as the closure of 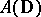in 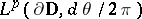(cf. also Hardy spaces). Let 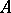be a Dirichlet algebra on 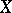and 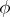a non-zero complex homomorphism o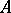f . If 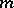is a representing measure on 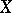for 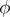, then 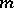is unique. For 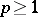, the abstract Hardy space 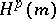is defined as the closure of 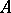in 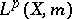. A lot of theorems for the Hardy space 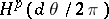are valid for the abstract Hardy space .

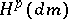Let 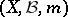be a probability measure space (cf. also Probability measure; Measure space), let 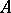be a subalgebra of 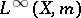containing the constants and let 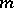be multiplicative on 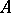. The algebra 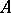is called a weak Dirichlet algebra if 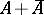is weak 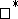dense in 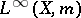. A Dirichlet algebra is a weak 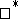Dirichlet algebra when 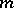is a representing measure on it. Weak Dirichlet algebras were introduced by T. Srinivasan and J. Wang [a9] as the smallest axiomatic setting on which each one of a lot of important theorems for the Hardy space 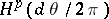are equivalent to the fact that 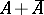is weak dense in .

K. Hoffman and H. Rossi [a6] gave an example such that even if 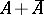is dense in 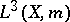, 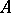is not a weak 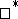Dirichlet algebra. Subsequently, it was shown [a6] that if 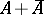is dense in 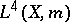, then 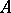is a weak Dirichlet algebra. W. Arveson [a1] introduced non-commutative weak Dirichlet algebras, which are also called subdiagonal algebras.

Examples of (weak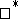) Dirichlet algebras.

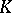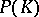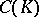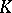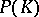Let be a compact subset of the complex plane and suppose the algebra consists of the functions in that can be approximated uniformly on by polynomials in . Then is a Dirichlet algebra on the outer boundary of 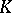[a2].

Let 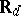be the real line 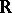endowed with the discrete topology and suppose the algebra 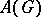consists of the functions in 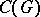whose Fourier coefficients are zero on the semi-group 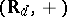, where 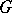is the compact dual group of 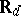. Then 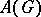is a Dirichlet algebra on 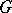[a5].

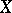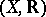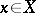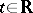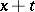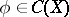Let be a fixed compact Hausdorff space upon which the real line (with the usual topology) acts as a locally compact transformation group. The pair is called a flow. The translate of an by a is written as . A is called analytic if for each 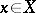the function 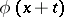of 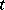is a boundary function which is bounded and analytic in the upper half-plane. If 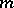is an invariant ergodic probability measure on 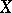, then 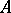is a weak 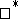Dirichlet algebra in 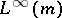[a7]. See also Hypo-Dirichlet algebra.

References

[a1]	W. Arveson, "Analyticity in operator algebras" Amer. J. Math. , 89 (1967) pp. 578–642
[a2]	H. Barbey, H. König, "Abstract analytic function theory and Hardy algebras" , Lecture Notes Math. : 593 , Springer (1977)
[a3]	T. Gamelin, J. Garnett, "Pointwise bounded approximation and Dirichlet algebras" J. Funct. Anal. , 8 (1971) pp. 360–404
[a4]	A. Gleason, "Function algebras" , Sem. Analytic Functions , II , Inst. Adv. Study Princeton (1957)
[a5]	H. Helson, "Analyticity on compact Abelian groups" , Algebras in Analysis; Proc. Instructional Conf. and NATO Adv. Study Inst., Birmigham, 1973 , Acad. Press (1975) pp. 1–62
[a6]	K. Hoffman, H. Rossi, "Function theory from a multiplicative linear functional" Trans. Amer. Math. Soc. , 102 (1962) pp. 507–544
[a7]	P. Muhly, "Function algebras and flows" Acta Sci. Math. , 35 (1973) pp. 111–121
[a8]	T. Nakazi, "Hardy spaces and Jensen measures" Trans. Amer. Math. Soc. , 274 (1982) pp. 375–378
[a9]	T. Srinivasan, J. Wang, "Weak-Dirichlet algebras, Function algebras" , Scott Foresman (1966) pp. 216–249
[a10]	J. Wermer, "Dirichlet algebras" Duke Math. J. , 27 (1960) pp. 373–381