Fourier algebra

Eymard algebra

Let 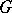be a locally compact group. The algebra 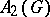(see also Figà-Talamanca algebra for notations) is called the Fourier algebra of 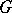. In fact,

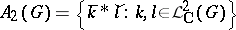and for ,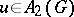

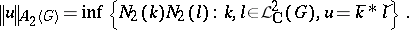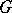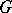Let be Abelian and let be the canonical mapping from onto 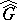. Then , where 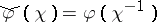, is an isometric isomorphism of the Banach algebra 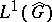onto 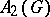. Therefore 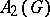can be considered as a substitute o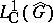f if 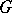is non-Abelian.

One always has 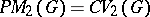: 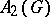is precisely the pre-dual of the von Neumann algebra 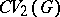. For the definition of 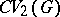and 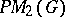, see Figà-Talamanca algebra. Consequently, in analogy with the Abelian case, 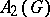is weakly 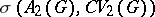sequentially complete.

The existence, for 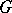not amenable, of approximate units in 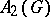is still in doubt (as of 2000). However, such exist for all closed subgroups of 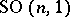and 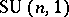. Such approximate units in 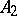can be used in the study of lattices of non-compact simple Lie groups of real rank one ([a1]).

For a study of certain ideals of 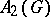, see [a2], [a4].

The unimodular case was first investigated by W.F. Stinespring, using a very interesting non-commutative integration theory [a6]. The case of a general locally compact group was initiated by P. Eymard [a3] on the basis of an extensive use of the theories of 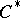-algebras and von Neumann algebras.

If 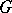is non-Abelian, 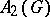is also called the Eymard algebra of 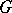and is denoted by .

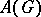See also Fourier–Stieltjes algebra.

References

[a1]	M. Cowling, U. Haagerup, "Completely bounded multipliers of the Fourier algebra of a simple Lie group of real rank one." Invent. Math. , 96 (1989) pp. 507–549
[a2]	J. Delaporte, A. Derighetti, "Best bounds for the approximate units of certain ideals 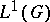of and of 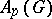" Proc. Amer. Math. Soc. , 124 (1996) pp. 1159–1169
[a3]	P. Eymard, "L'algèbre de Fourier d'un groupe localement compact" Bull. Soc. Math. France , 92 (1964) pp. 181–236
[a4]	E. Kaniuth, A.T. Lau, "A separation property of positive definite functions on locally compact groups and applications to Fourier algebras" J. Funct. Anal. , 175 (2000) pp. 89–110
[a5]	J.-P. Pier, "Amenable locally compact groups" , Wiley (1984)
[a6]	W.F. Stinespring, "Integration theorems for gages and duality for unimodular groups" Trans. Amer. Math. Soc. , 90 (1959) pp. 15–56