Bhatnagar-Gross-Krook model
BGK-model
Rarefied gas dynamics is described by the kinetic Boltzmann equation ([a13], [a6])
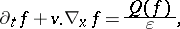 | (a1) |
where 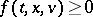 is the particle density in the phase space
is the particle density in the phase space 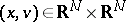 ,
,  is the mean free path and
is the mean free path and 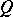 is the Boltzmann collision operator. This integral operator acts in the velocity variable
is the Boltzmann collision operator. This integral operator acts in the velocity variable  only, satisfies the moment relations
only, satisfies the moment relations
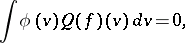 | (a2) |
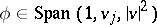 , and the entropy inequality
, and the entropy inequality
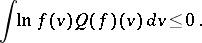 | (a3) |
These properties ensure the local conservation of mass, momentum and energy by integrating (a1) with respect to  ,
,
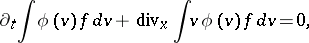 | (a4) |
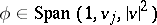 , and the decrease of entropy
, and the decrease of entropy
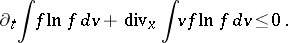 | (a5) |
Another striking property of the Boltzmann equation is that 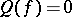 if and only if
if and only if 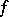 is a Maxwellian, that is
is a Maxwellian, that is
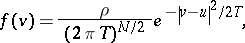 | (a6) |
for some 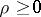 ,
, 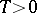 ,
, 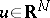 . When time and space dependence are allowed as in (a1),
. When time and space dependence are allowed as in (a1), 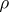 ,
, 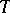 ,
,  can depend on
can depend on 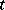 ,
,  also. When
also. When 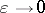 in (a1),
in (a1), 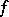 therefore goes formally to a Maxwellian of parameters
therefore goes formally to a Maxwellian of parameters 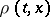 ,
, 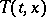 and
and 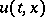 , see [a6], which satisfies the conservation laws (a4), and entropy inequality (a5), with
, see [a6], which satisfies the conservation laws (a4), and entropy inequality (a5), with 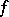 given by (a6). This system is the Euler system of mono-atomic perfect gas dynamics.
given by (a6). This system is the Euler system of mono-atomic perfect gas dynamics.
In their paper [a1], P.L. Bhatnagar, E.P. Gross, and M. Krook introduced a simplified Boltzmann-like model (called the BGK-model) which satisfies all the properties cited above. It is written in the form (a1) with
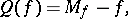 | (a7) |
and
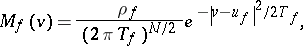 | (a8) |
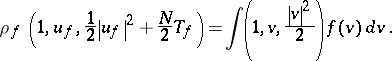 | (a9) |
The existence of a global solution to the BGK-model has been proved by B. Perthame [a14], and regularity properties are given in [a16]. Variations of the model are possible, by taking 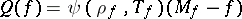 for some positive function
for some positive function 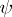 . The case
. The case 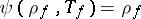 is of interest because then
is of interest because then 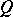 is quadratic, as is the Boltzmann operator. However, there is no existence result in this case.
is quadratic, as is the Boltzmann operator. However, there is no existence result in this case.
Many attempts have been done to generalize the BGK-formalism, in order to provide a natural kinetic description of hyperbolic systems of conservation laws, other than the Euler system of gas dynamics. Most of the known generalized BGK-models fit in the framework of [a2]. According to [a2], one writes
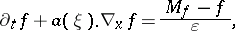 | (a10) |
where 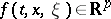 ,
,  ,
, 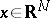 ,
, 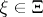 a measure space,
a measure space,  , and
, and
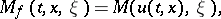 | (a11) |
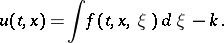 |
The equilibrium state 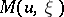 is assumed to satisfy
is assumed to satisfy
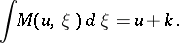 | (a12) |
Then, defining
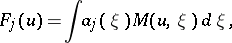 | (a13) |
the system relaxes as 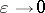 to the system of
to the system of 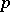 equations
equations
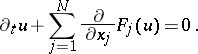 | (a14) |
Assume that  remains in a convex domain
remains in a convex domain 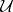 of
of 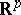 . An interesting property of the kinetic equation (a10) is that it leaves invariant any family of convex sets indexed by
. An interesting property of the kinetic equation (a10) is that it leaves invariant any family of convex sets indexed by 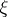 . Therefore if one chooses for each
. Therefore if one chooses for each 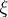 a convex set
a convex set 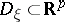 such that
such that
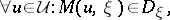 | (a15) |
then one can start with 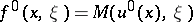 , for some
, for some 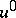 , and then
, and then 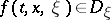 for all
for all 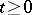 ,
,  ,
, 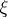 . The kinetic entropy inequality is obtained by a convex function
. The kinetic entropy inequality is obtained by a convex function 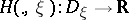 , such that the following Gibbs minimization principle holds: for any
, such that the following Gibbs minimization principle holds: for any 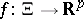 such that
such that 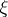 -a.e.
-a.e. 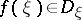 and
and 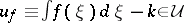 ,
,
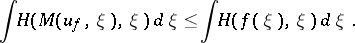 | (a16) |
This property ensures that in the limit 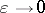 one obtains the entropy inequality
one obtains the entropy inequality
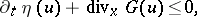 | (a17) |
with
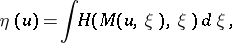 | (a18) |
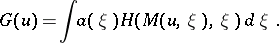 |
The original BGK-model (a1), (a7), (a8), (a9) enters this framework by taking  with Lebesgue measure,
with Lebesgue measure, 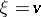 ,
, 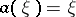 ,
, 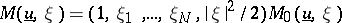 where
where 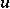 is the state and
is the state and 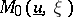 is the scalar physical Maxwellian given by (a6). One has
is the scalar physical Maxwellian given by (a6). One has 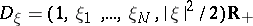 , and
, and 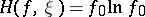 for any
for any 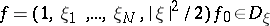 . Here, since
. Here, since 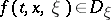 for all
for all 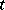 ,
,  ,
, 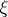 , the vector equation (a10) reduces to a scalar equation. It is also possible to treat polytropic gases by introducing internal energy, using the approach of [a15]. Then
, the vector equation (a10) reduces to a scalar equation. It is also possible to treat polytropic gases by introducing internal energy, using the approach of [a15]. Then 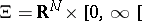 ,
, 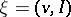 ,
, 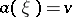 ,
,  ,
, 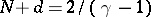 ,
, 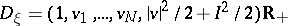 . See also [a10] for related models.
. See also [a10] for related models.
The success of such BGK-models has been revealed for scalar equations (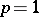 ) by Y. Brenier [a3], Y. Giga and T. Miyakawa [a8], and later by B. Perthame and E. Tadmor [a17], and by R. Natalini [a12]. It appears that in this case there is a so-called "kinetic formulation" , that is, an equation like (a10) but with
) by Y. Brenier [a3], Y. Giga and T. Miyakawa [a8], and later by B. Perthame and E. Tadmor [a17], and by R. Natalini [a12]. It appears that in this case there is a so-called "kinetic formulation" , that is, an equation like (a10) but with 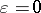 and the right-hand side being replaced by a suitable term, see [a11]. Another case where this holds can be found in [a4] and [a5]. More generally, BGK-models can be seen as a subclass of the general class of relaxation models, described for example in [a7], [a9].
and the right-hand side being replaced by a suitable term, see [a11]. Another case where this holds can be found in [a4] and [a5]. More generally, BGK-models can be seen as a subclass of the general class of relaxation models, described for example in [a7], [a9].
The BGK-model (a10) also exists in a time-discrete form, which appears in the literature as the transport-collapse method [a3], kinetic or Boltzmann schemes [a15], and which gives an approximate solution to (a14). It is an algorithm that gives 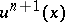 from the knowledge of
from the knowledge of 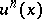 , by solving
, by solving
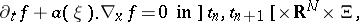 | (a19) |
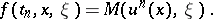 |
The new state 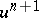 is given by
is given by
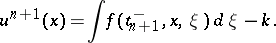 | (a20) |
Then,
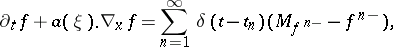 | (a21) |
which is similar to (a10) with  . The minimization principle (a16) ensures that a discrete entropy inequality holds.
. The minimization principle (a16) ensures that a discrete entropy inequality holds.
References
| [a1] | P.L. Bhatnagar, E.P. Gross, M. Krook, "A model for collision processes in gases" Phys. Rev. , 94 (1954) pp. 511 |
| [a2] | F. Bouchut, "Construction of BGK models with a family of kinetic entropies for a given system of conservation laws" J. Statist. Phys. , 95 (1999) pp. 113–170 |
| [a3] | Y. Brenier, "Averaged multivalued solutions for scalar conservation laws" SIAM J. Numer. Anal. , 21 (1984) pp. 1013–1037 |
| [a4] | Y. Brenier, L. Corrias, "A kinetic formulation for multi-branch entropy solutions of scalar conservation laws" Ann. Inst. H. Poincaré Anal. Non Lin. , 15 (1998) pp. 169–190 |
| [a5] | Y. Brenier, L. Corrias, R. Natalini, "A relaxation approximation to a moment hierarchy of conservation laws with kinetic formulation" preprint (1998) |
| [a6] | C. Cercignani, R. Illner, M. Pulvirenti, "The mathematical theory of dilute gases" Appl. Math. Sci. , 106 , Springer (1994) |
| [a7] | G.Q. Chen, C.D. Levermore, T.-P. Liu, "Hyperbolic conservation laws with stiff relaxation terms and entropy" Commun. Pure Appl. Math. , 47 (1994) pp. 787–830 |
| [a8] | Y. Giga, T. Miyakawa, "A kinetic construction of global solutions of first order quasilinear equations" Duke Math. J. , 50 (1983) pp. 505–515 |
| [a9] | S. Jin, Z.-P. Xin, "The relaxation schemes for systems of conservation laws in arbitrary space dimensions" Commun. Pure Appl. Math. , 48 (1995) pp. 235–276 |
| [a10] | C.D. Levermore, "Moment closure hierarchies for kinetic theories" J. Statist. Phys. , 83 (1996) pp. 1021–1065 |
| [a11] | P.-L. Lions, B. Perthame, E. Tadmor, "A kinetic formulation of multidimensional scalar conservation laws and related equations" J. Amer. Math. Soc. , 7 (1994) pp. 169–191 |
| [a12] | R. Natalini, "A discrete kinetic approximation of entropy solutions to multidimensional scalar conservation laws" J. Diff. Eq. , 148 (1998) pp. 292–317 |
| [a13] | C. Truesdell, R.G. Muncaster, "Fundamentals of Maxwell's kinetic theory of a simple monatomic gas, treated as a branch of rational mechanics" , Pure Appl. Math. , 83 , Acad. Press (1980) |
| [a14] | B. Perthame, "Global existence to the BGK model of Boltzmann equation" J. Diff. Eq. , 82 (1989) pp. 191–205 |
| [a15] | B. Perthame, "Boltzmann type schemes for gas dynamics and the entropy property" SIAM J. Numer. Anal. , 27 (1990) pp. 1405–1421 |
| [a16] | B. Perthame, M. Pulvirenti, "Weighted 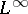 bounds and uniqueness for the Boltzmann BGK model" Arch. Rat. Mech. Anal. , 125 (1993) pp. 289–295 bounds and uniqueness for the Boltzmann BGK model" Arch. Rat. Mech. Anal. , 125 (1993) pp. 289–295 |
| [a17] | B. Perthame, E. Tadmor, "A kinetic equation with kinetic entropy functions for scalar conservation laws" Comm. Math. Phys. , 136 (1991) pp. 501–517 |
Bhatnagar-Gross-Krook model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bhatnagar-Gross-Krook_model&oldid=50259