Fuzzy topology
lattice-valued topology, point-set lattice-theoretic topology, poslat topology
A branch of mathematics encompassing any sort of topology using lattice-valued subsets. The following description is based on the standardization of this discipline undertaken in [a9], especially [a10], [a11]; much additional information is given in the references below.
Let 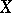 be a set and
be a set and 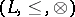 any complete quasi-monoidal lattice (a cqml; i.e.,
any complete quasi-monoidal lattice (a cqml; i.e., 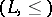 is a complete lattice with bottom element
is a complete lattice with bottom element 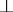 and top element
and top element 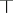 , and the tensor product
, and the tensor product 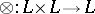 is isotone in both arguments with
is isotone in both arguments with 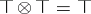 ). Examples of complete quasi-monoidal lattices are:
). Examples of complete quasi-monoidal lattices are:
complete lattices with 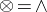 (binary meet);
(binary meet);
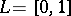 with
with 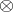 any of the
any of the 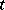 -norms
-norms 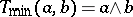 ,
, 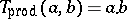 , or
, or 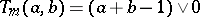 ; or
; or
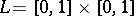 with
with 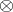 any of
any of 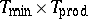 ,
, 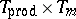 , etc.
, etc.
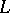 -subsets of
-subsets of 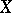 comprise the
comprise the 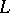 -powerset
-powerset 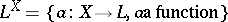 , a complete quasi-monoidal lattice via the lifting of the structure of
, a complete quasi-monoidal lattice via the lifting of the structure of 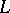 . A subfamily
. A subfamily 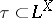 is an
is an 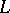 -topology on
-topology on 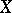 , and
, and 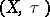 is an
is an 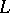 -topological space, if
-topological space, if  is closed under
is closed under 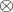 and arbitrary
and arbitrary 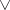 and contains the constant mapping
and contains the constant mapping 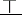 . A function
. A function 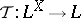 is an
is an 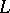 -fuzzy topology on
-fuzzy topology on 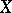 , and
, and 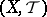 is an
is an 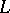 -fuzzy topological space, if
-fuzzy topological space, if 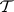 satisfies (reading
satisfies (reading 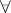 as "for each" ):
as "for each" ):
1) 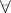 set
set 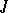 ,
, 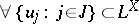 ,
,
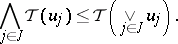 |
2)  two-element set
two-element set  ,
, 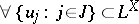 ,
,
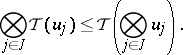 |
3) 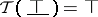 .
.
The member 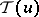 of
of 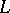 is interpreted as the "degree of openness" of
is interpreted as the "degree of openness" of  .
.
Important examples of 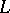 -topological and
-topological and 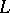 -fuzzy topological spaces can be found in [a5], Chap. 11; [a6], Kubiak's paper; [a8]; [a9], Chaps. 6, 8, 10; [a9], Chap. 7, Sect. 2.15–2.16; [a10], Sect. 7; [a11], Sect. 7.
-fuzzy topological spaces can be found in [a5], Chap. 11; [a6], Kubiak's paper; [a8]; [a9], Chaps. 6, 8, 10; [a9], Chap. 7, Sect. 2.15–2.16; [a10], Sect. 7; [a11], Sect. 7.
For a complete quasi-monoidal lattice 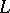 and function
and function 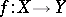 , one defines the powerset operators
, one defines the powerset operators 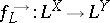 (the image operator) and
(the image operator) and 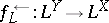 (the pre-image operator) by
(the pre-image operator) by
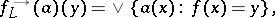 |
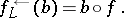 |
It is well-known that 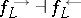 and that these operators generalize the traditional operators
and that these operators generalize the traditional operators 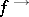 and
and 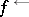 . Given
. Given 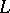 -topological spaces
-topological spaces 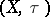 and
and 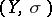 , a mapping
, a mapping 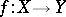 is
is 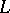 -continuous from
-continuous from 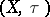 to
to 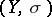 if
if 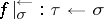 ; and given
; and given 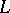 -fuzzy topological spaces
-fuzzy topological spaces 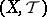 and
and 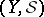 , a mapping
, a mapping 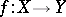 is
is  -fuzzy continuous from
-fuzzy continuous from 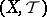 to
to 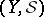 if
if 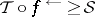 on
on 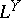 . The category
. The category 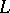 -
- comprises
comprises 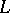 -topological spaces,
-topological spaces, 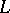 -continuous mappings, and the composition and identities from the category
-continuous mappings, and the composition and identities from the category 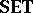 (cf. also Sets, category of); and the category
(cf. also Sets, category of); and the category 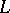 -
-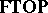 comprises
comprises 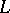 -fuzzy topological spaces,
-fuzzy topological spaces, 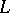 -fuzzy continuous mappings, and the composition and identities from the category
-fuzzy continuous mappings, and the composition and identities from the category 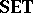 . It is a theorem that for all complete quasi-monoidal lattices
. It is a theorem that for all complete quasi-monoidal lattices 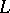 , the categories
, the categories 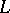 -
- and
and 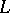 -
-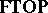 are topological categories over
are topological categories over 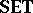 , in the sense of [a3] and [a11], Sect. 1, and hence topological constructs.
, in the sense of [a3] and [a11], Sect. 1, and hence topological constructs.
The above briefly describes "fixed-basis topology" — topology where the complete quasi-monoidal lattice 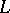 , viewed as the lattice-theoretic base of powersets
, viewed as the lattice-theoretic base of powersets 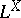 and spaces
and spaces 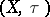 or
or 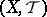 , is fixed relative to the spaces and mappings of the category
, is fixed relative to the spaces and mappings of the category 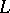 -
- or
or 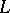 -
-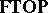 . "Variable-basis topology" permits the base to change within a category, so that each space has its own lattice-theoretic base.
. "Variable-basis topology" permits the base to change within a category, so that each space has its own lattice-theoretic base.
To outline variable-basis topology, note that all complete quasi-monoidal lattices form a category, 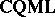 , in which morphisms are mappings preserving
, in which morphisms are mappings preserving 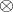 , arbitrary
, arbitrary 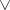 , and
, and 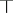 ; and also note that
; and also note that  and
and 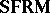 embed into
embed into 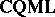 . One then considers
. One then considers 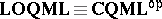 , with objects the same as those of
, with objects the same as those of 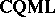 , now called localic quasi-monoidal lattices, but morphisms reversed from those of
, now called localic quasi-monoidal lattices, but morphisms reversed from those of 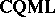 ; and one notes that
; and one notes that 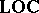 and
and 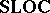 embed into
embed into 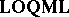 .
.
Now, let 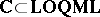 . The category
. The category 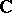 -
- for variable-basis topology and the category
for variable-basis topology and the category 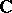 -
-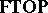 for variable-basis fuzzy topology are both "concrete" categories over
for variable-basis fuzzy topology are both "concrete" categories over 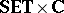 as a "ground" or "base" category. For a
as a "ground" or "base" category. For a 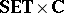 morphism
morphism 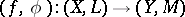 , the pre-image operator
, the pre-image operator 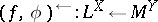 is defined by
is defined by 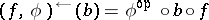 . An image operator
. An image operator 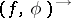 is also available which, if
is also available which, if 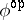 preserves arbitrary
preserves arbitrary 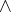 , satisfies
, satisfies 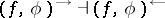 ; and if
; and if 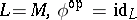 , these operators reduce to their fixed-basis counterparts.
, these operators reduce to their fixed-basis counterparts.
Data for the category 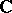 -
- include:
include:
objects are topological spaces  (cf. also Topological space), where
(cf. also Topological space), where 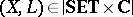 and
and 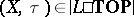 ;
;
morphisms are continuous mappings
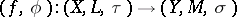 |
(cf. also Continuous function), where 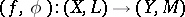 is in
is in 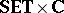 and
and 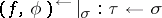 .
.
Data for the category 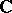 -
-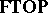 include:
include:
objects are fuzzy topological spaces 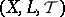 , where
, where 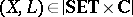 and
and 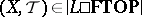 ;
;
morphisms are fuzzy continuous mappings 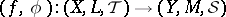 , where
, where 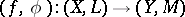 is in
is in 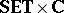 and
and 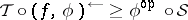 on
on 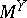 .
.
In both categories, compositions and identities are those of 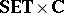 .
.
It is a theorem that for all 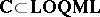 ,
, 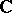 -
- and
and 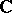 -
-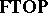 are topological over the ground
are topological over the ground 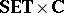 in the sense of [a3] and [a11], Sect. 1. Further, these frameworks unify all the fixed-basis categories for topology given above and hence unify all important examples (referenced above) over different lattice-theoretic bases (e.g. two fuzzy real lines
in the sense of [a3] and [a11], Sect. 1. Further, these frameworks unify all the fixed-basis categories for topology given above and hence unify all important examples (referenced above) over different lattice-theoretic bases (e.g. two fuzzy real lines 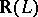 and
and 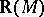 ). Moreover, all purely lattice-theoretic or point-free approaches to topology — locales, topological molecular lattices, uniform lattices, etc. (see [a1], [a2], [a8]) — categorically embed into
). Moreover, all purely lattice-theoretic or point-free approaches to topology — locales, topological molecular lattices, uniform lattices, etc. (see [a1], [a2], [a8]) — categorically embed into 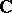 -
- or
or 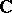 -
-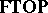 (for appropriate
(for appropriate 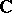 ) as subcategories of singleton spaces; e.g.
) as subcategories of singleton spaces; e.g.  embeds as singleton spaces into
embeds as singleton spaces into 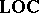 -
- . Thus, the variable-basis approach categorically unifies topology and fuzzy topology as a discipline.
. Thus, the variable-basis approach categorically unifies topology and fuzzy topology as a discipline.
References
| [a1] | P.T. Johnstone, "Stone spaces" , Cambridge Univ. Press (1982) |
| [a2] | G.-J. Wang, "Theory of L-fuzzy topological spaces" , Shanxi Normal Univ. Publ. House (1988) (In Chinese) |
| [a3] | J. Adamek, H. Herrlich, G.E. Strecker, "Abstract and concrete categories" , Wiley (1990) |
| [a4] | U. (ed.) Höhle, "Mathematical aspects of fuzzy set theory" Fuzzy Sets and Syst. , 40 : 2 (1991) (Special Memorial Volume–Second Issue) |
| [a5] | "Applications of category theory to fuzzy subsets" S.E. Rodabaugh (ed.) E.P. Klement (ed.) U. Höhle (ed.) , Kluwer Acad. Publ. (1992) |
| [a6] | U. Höhle, S.E. Rodabaugh, A. (eds.) Šostak, "Special issue on fuzzy topology" Fuzzy Sets and Syst. , 73 : 1 (1995) |
| [a7] | W. (ed.) Kotzé, "Special issue" Quaestiones Math. , 20 : 3 (1997) |
| [a8] | Liu Ying–Ming, Luo Mao–Kang, "Fuzzy topology" , World Sci. (1997) |
| [a9] | "Mathematics of fuzzy sets: Logic, topology, and measure theory" U. Höhle (ed.) S.E. Rodabaugh (ed.) , The Handbooks of Fuzzy Sets , 3 , Kluwer Acad. Publ. (1999) |
| [a10] | U. Höhle, A. Šostak, "Axiomatic foundations of fixed-basis fuzzy topology" U. Höhle (ed.) S.E. Rodabaugh (ed.) , Mathematics of Fuzzy Sets: Logic, Topology, and Measure Theory , The Handbooks of Fuzzy Sets , 3 , Kluwer Acad. Publ. (1999) pp. 123–272 |
| [a11] | S.E. Rodabaugh, "Categorical foundations of variable-basis fuzzy topology" U. Höhle (ed.) S.E. Rodabaugh (ed.) , Mathematics of Fuzzy Sets: Logic, Topology, and Measure Theory , The Handbooks of Fuzzy Sets , 3 , Kluwer Acad. Publ. (1999) pp. 273–388 |
Fuzzy topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fuzzy_topology&oldid=50222