Turán number

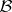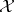A collection of subsets of size ( "blocks" ) of a ground set of size is said to form a Turán 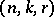-system if each 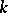-element subset of 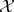contains at least one block. The Turán number 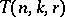is the minimum size of such a collection. P. Turán introduced these numbers in [a6]. The related dual notion is that of the covering number 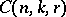, defined to be the smallest number of blocks needed to cover (by inclusion) each 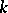-element subset. Several recursions are known; e.g. in [a2] it is shown that

Also, the limit

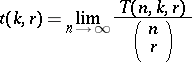is known to exist, though the values of 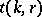are known only for 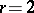. These facts and the ones that follow are based on an extensive survey by A. Sidorenko ([a5]):

i) .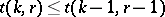

ii) [a1].

iii) It has been conjectured that 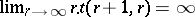[a1].

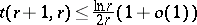iv) [a4].

v) 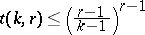[a3]. The situation of small 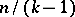has been studied extensively, as have been the cases 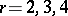. The case of small 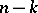is also well-studied; this leads to the covering number. See [a5] for details.

References

[a1]	D. de Caen, "Extension of a theorem of Moon and Moser on complete subgraphs" Ars Combinatoria , 16 (1983) pp. 5–10
[a2]	G. Katona, T. Nemetz, M. Simonovits, "On a graph problem of Turán" Mat. Lapok , 15 (1964) pp. 228–238
[a3]	A. Sidorenko, "Systems of sets that have the 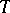-property" Moscow Univ. Math. Bull. , 36 (1981) pp. 22–26
[a4]	A. Sidorenko, "Upper bounds on Turán numbers" J. Combin. Th. A , 77 : 1 (1997) pp. 134–147
[a5]	A. Sidorenko, "What we know and what we do not know about Turán numbers" Graphs Combin. , 11 (1995) pp. 179–199
[a6]	P. Turán, "Research Problems" Magyar Tud. Akad. Mat. Kutato Internat. Közl. , 6 (1961) pp. 417–423