Conway algebra
An abstract algebra which yields an invariant of links in 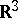 (cf. also Link).
(cf. also Link).
The concept is related to the entropic right quasi-group (cf. also Quasi-group). A Conway algebra consists of a sequence of  -argument operations (constants)
-argument operations (constants) 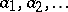 and two
and two  -argument operations
-argument operations  and
and  , which satisfy the following conditions:
, which satisfy the following conditions:
Initial conditions:
C1) 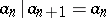 ;
;
C2) 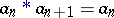 .
.
Transposition properties:
C3) 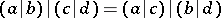 ;
;
C4)  ;
;
C5) 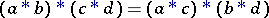 .
.
Inverse operation properties:
C6) 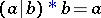 ;
;
C7) 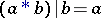 . The main link invariant yielded by a Conway algebra is the Jones–Conway polynomial, [a2], [a5], [a4].
. The main link invariant yielded by a Conway algebra is the Jones–Conway polynomial, [a2], [a5], [a4].
A nice example of a four-element Conway algebra, which leads to the link invariant distinguishing the left-handed and right-handed trefoil knots (cf. also Torus knot) is described below:
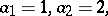 |
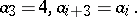 |
The operations  and
and  are given by the following tables:'
are given by the following tables:'
<tbody> </tbody>
|
'
<tbody> </tbody>
|
If one allows partial Conway algebras, one also gets the Murasugi signature and Tristram–Levine signature of links [a3]. The skein calculus (cf. also Skein module), developed by J.H. Conway, leads to the universal partial Conway algebra.
Invariants of links, 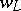 , yielded by (partial) Conway algebras have the properties that for the Conway skein triple
, yielded by (partial) Conway algebras have the properties that for the Conway skein triple 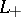 ,
, 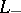 and
and 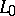 :
:
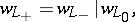 |
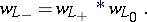 |
References
| [a1] | J.H. Conway, "An enumeration of knots and links" J. Leech (ed.) , Computational Problems in Abstract Algebra , Pergamon (1969) pp. 329–358 |
| [a2] | J.H. Przytycki, P. Traczyk, "Invariants of links of Conway type" Kobe J. Math. , 4 (1987) pp. 115–139 |
| [a3] | J.H. Przytycki, P. Traczyk, "Conway algebras and skein equivalence of links" Proc. Amer. Math. Soc. , 100 : 4 (1987) pp. 744–748 |
| [a4] | A.S. Sikora, "On Conway algebras and the Homflypt polynomial" J. Knot Th. Ramifications , 6 : 6 (1997) pp. 879–893 |
| [a5] | J.D. Smith, "Skein polynomials and entropic right quasigroups Universal algebra, quasigroups and related systems (Jadwisin 1989)" Demonstratio Math. , 24 : 1–2 (1991) pp. 241–246 |
Conway algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conway_algebra&oldid=50193

