Tail triviality
Let 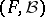 be a measurable space. A sequence of random variables
be a measurable space. A sequence of random variables 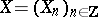 taking values in
taking values in 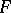 is described by the triple
is described by the triple 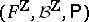 , where
, where 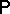 is a probability measure on
is a probability measure on 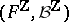 called the distribution of
called the distribution of 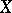 . The sequence
. The sequence 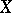 is said to be independent if
is said to be independent if 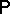 is a product measure, i.e.
is a product measure, i.e. 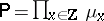 for probability measures
for probability measures  on
on  .
.
The right and left tail-sigma-fields of 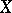 are defined as
are defined as
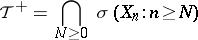 |
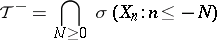 |
and the two-sided tail-sigma-field is defined as
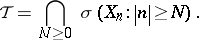 |
(Here, 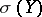 denotes the smallest sigma-field (cf. Borel field of sets) with respect to which
denotes the smallest sigma-field (cf. Borel field of sets) with respect to which 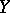 is measurable.) The Kolmogorov zero-one law [a1] states that, in the independent case,
is measurable.) The Kolmogorov zero-one law [a1] states that, in the independent case, 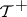 ,
,  and
and 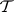 are trivial, i.e. all their elements have probability
are trivial, i.e. all their elements have probability  or
or 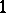 under
under  . Without the independence property this need no longer be true: tail triviality only holds when
. Without the independence property this need no longer be true: tail triviality only holds when  has sufficiently weak dependencies. In fact, when the index set
has sufficiently weak dependencies. In fact, when the index set 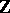 is viewed as time, tail triviality means that the present is asymptotically independent of the far future and the far past. There exist examples where
is viewed as time, tail triviality means that the present is asymptotically independent of the far future and the far past. There exist examples where  ,
, 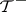 are trivial but
are trivial but 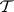 is not [a3]. Intuitively, in such examples there are "dependencies across infinity" .
is not [a3]. Intuitively, in such examples there are "dependencies across infinity" .
Instead of indexing the random variables by 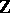 one may also consider a random field
one may also consider a random field 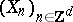 , indexed by the
, indexed by the 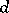 -dimensional integers (
-dimensional integers (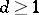 ). The definition of
). The definition of 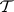 is the same as before, but now with
is the same as before, but now with 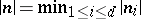 , and
, and 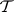 is called the sigma-field at infinity. For independent random fields,
is called the sigma-field at infinity. For independent random fields, 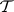 is again trivial. Without the independence property, however, the question is considerably more subtle and is related to the phenomenon of phase transition (i.e. non-uniqueness of probability measures having prescribed conditional probabilities in finite sets). Tail triviality holds, for instance, when
is again trivial. Without the independence property, however, the question is considerably more subtle and is related to the phenomenon of phase transition (i.e. non-uniqueness of probability measures having prescribed conditional probabilities in finite sets). Tail triviality holds, for instance, when 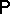 is an extremal Gibbs measure [a2].
is an extremal Gibbs measure [a2].
References
| [a1] | P. Billingsley, "Probability and measure" , Wiley (1986) (Edition: Second) |
| [a2] | H.-O. Georgii, "Gibbs measures and phase transitions" , Studies Math. , 9 , W. de Gruyter (1988) |
| [a3] | D.S. Ornstein, B. Weiss, "Every transformation is bilaterally deterministic" Israel J. Math. , 24 (1975) pp. 154–158 |
Tail triviality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tail_triviality&oldid=50128