Carleson measure

Carleson measures were introduced in the early 1960s by L. Carleson [a1] to characterize the interpolating sequences in the algebra of bounded analytic functions in the open unit disc and to give a solution to the corona problem (cf. also Hardy spaces).

These measures can be defined in the following way: Let be a positive measure on the unit disc . Then is called a Carleson measure if there exists a constant such that for every sector

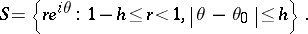Carleson measures play an important role in complex analysis (cf. also Analytic function), harmonic analysis, theory (cf. also -space), the theory of integral operators, and the theory of 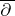-equations (cf. also Neumann 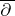-problem). One of Carleson's original theorems states that, with 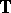denoting the boundary of 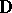, for the Poisson operator (cf. also Poisson integral)

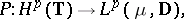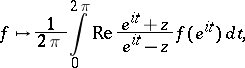is a bounded linear operator from the Hardy space 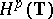to 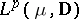if and only if 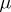is a Carleson measure. Generalizations of this principle to various other function spaces in one or several real or complex variables have been given. Carleson measures and their generalizations can also be used to give complete characterizations of boundedness and compactness of composition operators on various spaces of analytic functions, such as Hardy and Bergman spaces (see [a2]).

References

[a1]	L. Carleson, "Interpolation by bounded analytic functions and the corona problem" Ann. of Math. , 76 (1962) pp. 347–559
[a2]	C. Cowen, B. MacCluer, "Composition operators on spaces of analytic functions" , CRC (1995)