Hermann algorithms
In her famous 1926 paper [a6], G. Hermann set out to show that all standard objects in the theory of polynomial ideals over fields 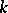 , including the prime ideals associated to a given ideal, can be determined by means of computations involving finitely many steps, i.e. field operations in
, including the prime ideals associated to a given ideal, can be determined by means of computations involving finitely many steps, i.e. field operations in 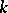 . Any
. Any 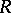 -module for
-module for  is determined by giving a finite set of generators, called a basis. Hermann states explicitly that one can give an upper bound for the number of operations necessary for each sort of computation.
is determined by giving a finite set of generators, called a basis. Hermann states explicitly that one can give an upper bound for the number of operations necessary for each sort of computation.
Building on previous work [a7] by K. Henzelt and E. Noether, Hermann's work set a milestone in effective algebra. While the structural approach to algebra continued to flourish, Hermann's contribution lay fallow for decades except mainly for the notice of a few gaps:
Condition (F): B.L. van der Waerden pointed out in [a10] that it is necessary to assume that one can completely factor an arbitrary polynomial over 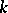 .
.
Condition (P): A. Seidenberg pointed out in [a1] that, in characteristic 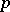 , it is necessary to assume roughly the decidability of whether
, it is necessary to assume roughly the decidability of whether 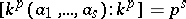 .
.
Condition (F ): M. Reufel pointed out in [a9] that, in order to obtain a normal basis for a finitely-generated free module over a polynomial ring, one needs only the factorization of polynomials into prime powers. This is weaker than (F) in positive characteristic.
): M. Reufel pointed out in [a9] that, in order to obtain a normal basis for a finitely-generated free module over a polynomial ring, one needs only the factorization of polynomials into prime powers. This is weaker than (F) in positive characteristic.
Numerical corrections: C. Veltzke, cf. [a2], [a3], (and later Seidenberg [a1] and D. Lazard [a4]) noted and removed numerical inaccuracies in Hermann's bounds. The conditions are vital in Hermann's manipulations of "Elementarteilerformen" (Chow forms).
Starting in mid-twentieth century, the work of W. Krull [a11], A. Fröhlich and J.C. Sheperdson [a5], Reufel [a9], and Lazard [a4] made even more explicit that Hermann's computations give an algorithm. For more detailed historical remarks and a complete bibliography up to 1980, see [a2], [a3]. Nowadays (as of 2000), the main practical methods for computation in commutative algebra are implemented using Gröbner bases (cf. also Gröbner basis).
However, even from a thoroughly modern point of view, Hermann's algorithm for linear algebra over 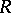 retains interest because it gives directly the correct order of magnitude of complexity of the fundamental membership problem over
retains interest because it gives directly the correct order of magnitude of complexity of the fundamental membership problem over  . That algorithm is embodied in the following basic result.
. That algorithm is embodied in the following basic result.
Let 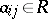 have degree at most
have degree at most 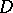 ,
, 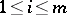 ,
, 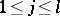 . An
. An 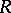 -basis for the solutions
-basis for the solutions 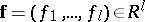 of the related homogeneous system of equations
of the related homogeneous system of equations
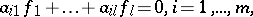 |
can be determined in a finite number of steps. That basis will have entries whose degrees are bounded by a function 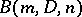 satisfying the recursion
satisfying the recursion
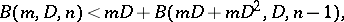 |
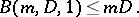 |
To see this, let 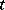 be a new indeterminate over
be a new indeterminate over 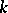 . If
. If 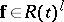 is a solution of the system, one can clear out the denominators to assume that
is a solution of the system, one can clear out the denominators to assume that 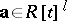 . Then the coefficients of each fixed power of
. Then the coefficients of each fixed power of 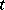 give a solution. So a basis of solutions over
give a solution. So a basis of solutions over 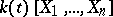 leads to a basis of solutions over
leads to a basis of solutions over 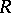 , with the same bounds, and one can assume that
, with the same bounds, and one can assume that 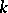 is infinite.
is infinite.
One may re-index the equations and unknowns, if necessary, to arrange that the upper left 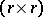 -submatrix of coefficients has maximal rank
-submatrix of coefficients has maximal rank  . Set
. Set
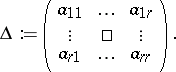 |
Now, since 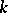 is infinite, one may arrange by a change of variables
is infinite, one may arrange by a change of variables 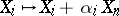 ,
, 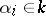 , that
, that 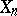 occurs in
occurs in 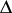 with exponent equal to
with exponent equal to 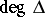 . Next one may apply Cramer's rule (cf. Cramer rule) to think of the original system of equations as being of the form:
. Next one may apply Cramer's rule (cf. Cramer rule) to think of the original system of equations as being of the form:
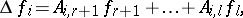 |
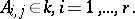 |
Subtracting as necessary multiples of the obvious solutions
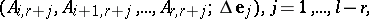 |
where 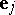 denotes the
denotes the 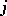 th standard basis element of
th standard basis element of 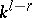 , allows one to restrict the search for possible further solutions to those with
, allows one to restrict the search for possible further solutions to those with
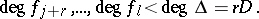 |
Thus, for these remaining solutions one may bound the degrees of all 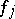 with respect to
with respect to 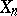 by
by 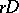 , and hence one may think of the
, and hence one may think of the 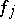 as linear combinations of
as linear combinations of 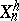 ,
, 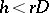 , with coefficients from
, with coefficients from 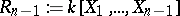 . Setting to zero the coefficients of the resulting
. Setting to zero the coefficients of the resulting  powers of
powers of 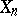 from the original system of equations gives a linear homogeneous system of at most
from the original system of equations gives a linear homogeneous system of at most 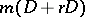 equations with coefficients from
equations with coefficients from 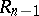 of degree at most
of degree at most 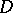 .
.
Tracing through the argument verifies the recurrence. It is easy to verify that when 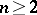 ,
,
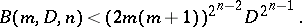 |
For consistent systems of inhomogeneous equations, Cramer's rule gives a particular solution, and the above procedure gives a basis for the related homogeneous system: One can determine in a finite number of steps whether a given system of 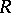 -linear inhomogeneous equations
-linear inhomogeneous equations
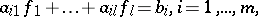 |
has a solution 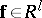 . If it does, one can be found in a finite number steps with
. If it does, one can be found in a finite number steps with  .
.
Thus, the Hermann algorithm gives explicit bounds for the ideal membership problem. According to the examples in [a8], such bounds are necessarily doubly exponential. This is in contrast with the singly exponential bounds for the Hilbert Nullstellensatz (cf. Effective Nullstellensatz).
References
| [a1] | A. Seidenberg, "Constructions in algebra" Trans. Amer. Math. Soc. , 197 (1974) pp. 273–313 |
| [a2] | B. Renschuch, "Beiträge zur konstruktiven Theorie der Polynomideale XVII/1: Zur Henzelt/Noether/Hermannschen Theorie der endlich vielen Schritte" Wiss. Z. Pädagog. Hochsch. Karl Liebknecht, Potsdam , 24 (1980) pp. 87–99 |
| [a3] | B. Renschuch, "Beiträge zur konstruktiven Theorie der Polynomideale XVII/2: Zur Henzelt/Noether/Hermannschen Theorie der endlich vielen Schritte" Wiss. Z. Pädagog. Hochsch. Karl Liebknecht, Potsdam , 25 (1981) pp. 125–136 |
| [a4] | D. Lazard, "Algèbre linéaire sur  et élimination" Bull. Soc. Math. France , 105 (1977) pp. 165–190 et élimination" Bull. Soc. Math. France , 105 (1977) pp. 165–190 |
| [a5] | A. Fröhlich, J.C. Sheperdson, "Effective procedures in field theory" Philos. Trans. Royal Soc. A , 248 (1956) pp. 407–432 |
| [a6] | G. Hermann, "Die Frage der endlich vielen Schritte in der Theorie der Polynomideale" Math. Ann. , 95 (1926) pp. 736–788 |
| [a7] | K. Henzelt, "Zur Theorie der Polynomideale und Resultanten, bearbeitet von Emmy Noether" Math. Ann. , 88 (1923) pp. 53–79 |
| [a8] | E.W. Mayr, A.R. Meyer, "Complexity of the word problems for commutative semigroups and polynomial ideals" Adv. Math. , 46 (1982) pp. 305–329 |
| [a9] | M. Reufel, "Konstruktionsverfahren bei Moduln über Polynomringen" Math. Z. , 90 (1965) pp. 231–250 |
| [a10] | B.L. van der Waerden, "Eine Bemerkung über die Unzerlegbarkeit von Polynomen" Math. Ann. , 102 (1930) pp. 738–739 |
| [a11] | W. Krull, "Parameterspezialisierung in Polynomringen" Archiv Math. , 1 (1948/49) pp. 57–60 |
Hermann algorithms. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermann_algorithms&oldid=50112