Diagram(2)

Let and be directed graphs (also called oriented graphs, diagram schemes or pre-categories; cf. also Graph, oriented). A diagram of shape (also called a diagram of type) in is a morphism of graphs ; i.e. if and are given by

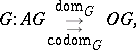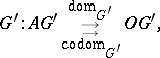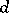(here and denote, respectively, a set of objects and a set of arrows of ), then a morphism is a pair of mappings

with , .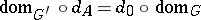

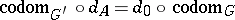A diagram is called finite if its shape is a finite graph, i.e. 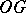and are finite sets. A diagram in a category 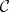is defined as a diagram , where 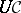denotes the underlying graph of 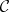(with the same objects and arrows, forgetting which arrows are composites and which are identities).

Every functor 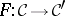is also a diagram between the corresponding graphs. This observation defines the forgetful functor 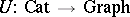from small categories to small graphs (cf. also Functor).

Let 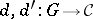be two diagrams of the same shape 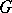in the same category 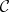. A morphism between 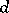and is a mapping 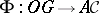that carries each object 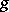of the graph 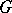to an arrow 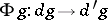, such that for any arrow 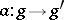of 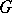the diagram

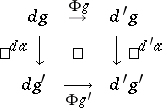commutes.

All diagrams of the shape 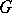in 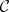and all morphisms between them form a category.

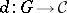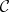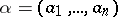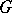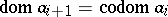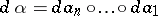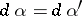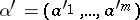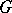Let be a diagram in the category and let be a finite sequence of arrows of the graph with , . Put . A diagram is called commutative if for any finite sequence in with , , , .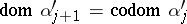

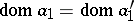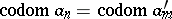A sequence is a diagram , where 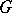is of the form

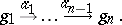The corresponding diagram is represented by

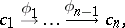where 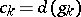are objects and are arrows of .

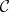A triangle diagram in the category is a diagram with shape graph

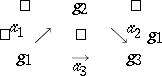and is represented as

Commutativity means that .

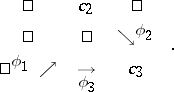
A quadratic diagram (also called a square diagram) in corresponds to the graph

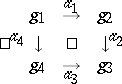and is represented as

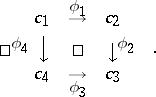Commutativity means .

References

[a1]	P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967)
[a2]	A. Grothendieck, "Sur quelques points d'algebre homologique" Tôhoku Math. J. Ser. II , 9 (1957) pp. 120–221
[a3]	S. Maclane, "Categories for the working mathematician" , Springer (1971)