X-inner derivation

The obvious Lie analogue of an 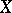-inner automorphism.

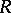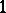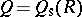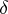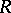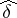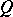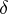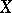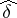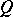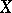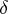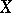Let be a prime ring (with ) and let denote its symmetric Martindale ring of quotients. Then any derivation of (cf. also Derivation in a ring) extends uniquely to a derivation of , and one says that is -inner if is inner on (cf. also -inner automorphism). It follows easily that is -inner if there exists a 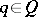with 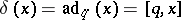for all 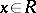. Of course, 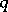is determined by 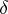up to an additive term in the extended centroid 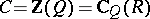. If 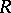is semi-prime (cf. also Prime ring), the definition is similar, but considerably more complicated.

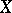-inner derivations are a tool in the study of differential identities, Galois theory with derivations, and enveloping algebra smash products. To start with, [a1] and [a2] show that the multi-linear differential identities of a semi-prime ring follow from generalized identities, where no derivations are involved, and from certain equations which are always satisfied by derivations. As a consequence, a prime ring satisfying a non-trivial differential identity must also satisfy a non-trivial generalized identity.

Next, let 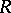be a prime ring of characteristic 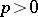and let 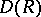denote the set of all derivations 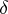of 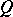such that 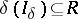for some 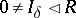. Then 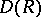is a restricted Lie ring (cf. also Lie algebra) which is a left 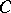-vector space, and [a3] and [a4] study the Galois theory of 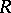determined by finite-dimensional restricted Lie subrings of 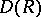. Specifically, [a3] considers the 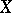-outer case, where 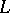contains no non-zero inner derivation of 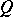, and [a4] assumes that 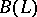, the 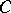-subalgebra of 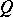generated by all 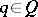with 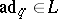, is quasi-Frobenius (cf. also Quasi-Frobenius ring). Note that, if 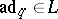, then 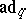is (essentially) an 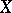-inner derivation of .

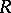Finally, 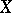-inner derivations appear in [a5] and [a6], where the prime ideals of certain enveloping algebra smash products 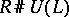are described.

References

[a1]	V.K. Kharchenko, "Differential identities of prime rings" Algebra and Logic , 17 (1979) pp. 155–168 Algebra i Logika , 17 (1978) pp. 220–238
[a2]	V.K. Kharchenko, "Differential identities of semiprime rings" Algebra and Logic , 18 (1979) pp. 58–80 Algebra i Logika , 18 (1979) pp. 86–119
[a3]	V.K. Kharchenko, "Constants of derivations of prime rings" Math. USSR Izv. , 45 (1982) pp. 381–401 Izv. Akad. Nauk SSSR Ser. Mat. , 45 (1981) pp. 435–461
[a4]	V.K. Kharchenko, "Derivations of prime rings of positive characteristic" Algebra and Logic , 35 (1996) pp. 49–58 Algebra i Logika , 35 (1996) pp. 88–104
[a5]	D.S. Passman, "Prime ideals in enveloping rings" Trans. Amer. Math. Soc. , 302 (1987) pp. 535–560
[a6]	D.S. Passman, "Prime ideals in restricted enveloping rings" Commun. Algebra , 16 (1988) pp. 1411–1436