Heat content asymptotics
Let  be a compact Riemannian manifold with boundary
be a compact Riemannian manifold with boundary  . Assume given a decomposition of the boundary as the disjoint union of two closed sets
. Assume given a decomposition of the boundary as the disjoint union of two closed sets  and
and  . Impose Neumann boundary conditions on
. Impose Neumann boundary conditions on  and Dirichlet boundary conditions on
and Dirichlet boundary conditions on  . Let
. Let  be the temperature distribution of the manifold corresponding to an initial temperature
be the temperature distribution of the manifold corresponding to an initial temperature  ;
;  is the solution to the equations:
is the solution to the equations:
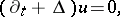 |
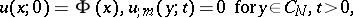 |
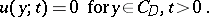 |
Here, 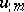 denotes differentiation with respect to the inward unit normal. Let
denotes differentiation with respect to the inward unit normal. Let  be a smooth function giving the specific heat. The total heat energy content of
be a smooth function giving the specific heat. The total heat energy content of 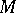 is given by
is given by
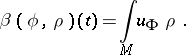 |
As 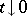 , there is an asymptotic expansion
, there is an asymptotic expansion
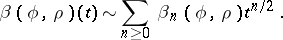 |
The coefficients 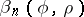 are the heat content asymptotics and are locally computable.
are the heat content asymptotics and are locally computable.
These coefficients were first studied with  empty and with
empty and with 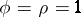 . Planar regions with smooth boundaries were studied in [a5], [a6], the upper hemisphere was studied in [a4], [a3], and polygonal domains in the plane were studied in [a7]. See [a11], [a12] for recursive formulas on a general Riemannian manifold.
. Planar regions with smooth boundaries were studied in [a5], [a6], the upper hemisphere was studied in [a4], [a3], and polygonal domains in the plane were studied in [a7]. See [a11], [a12] for recursive formulas on a general Riemannian manifold.
More generally, let  be the second fundamental form and let
be the second fundamental form and let 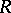 be the Riemann curvature tensor. Let indices
be the Riemann curvature tensor. Let indices  ,
,  ,
,  range from
range from 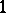 to
to  and index an orthonormal frame for the tangent bundle of the boundary. Let ":" (respectively, ";" ) denote covariant differentiation with respect to the Levi-Civita connection of
and index an orthonormal frame for the tangent bundle of the boundary. Let ":" (respectively, ";" ) denote covariant differentiation with respect to the Levi-Civita connection of  (respectively, of
(respectively, of 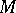 ) summed over repeated indices. The first few coefficients have the form:
) summed over repeated indices. The first few coefficients have the form:
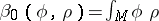 ;
;
 ;
;
 |
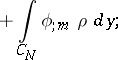 |
 |
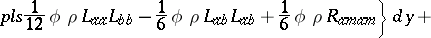 |
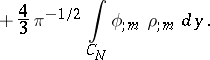 |
The coefficient 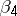 is known.
is known.
The coefficients  and
and 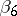 have been determined if
have been determined if  is empty.
is empty.
One can replace the Laplace operator  by an arbitrary operator of Laplace type as the evolution operator [a1], [a2], [a10], [a9]. One can study non-minimal operators as the evolution operator, inhomogeneous boundary conditions, and time-dependent evolution operators of Laplace type. A survey of the field is given in [a8].
by an arbitrary operator of Laplace type as the evolution operator [a1], [a2], [a10], [a9]. One can study non-minimal operators as the evolution operator, inhomogeneous boundary conditions, and time-dependent evolution operators of Laplace type. A survey of the field is given in [a8].
References
| [a1] | M. van den Berg, S. Desjardins, P. Gilkey, "Functoriality and heat content asymptotics for operators of Laplace type" Topol. Methods Nonlinear Anal. , 2 (1993) pp. 147–162 |
| [a2] | M. van den Berg, P. Gilkey, "Heat content asymptotics of a Riemannian manifold with boundary" J. Funct. Anal. , 120 (1994) pp. 48–71 |
| [a3] | M. van den Berg, P. Gilkey, "Heat invariants for odd dimensional hemispheres" Proc. R. Soc. Edinburgh , 126A (1996) pp. 187–193 |
| [a4] | M. van den Berg, "Heat equation on a hemisphere" Proc. R. Soc. Edinburgh , 118A (1991) pp. 5–12 |
| [a5] | M. van den Berg, E.M. Davies, "Heat flow out of regions in  " Math. Z. , 202 (1989) pp. 463–482 " Math. Z. , 202 (1989) pp. 463–482 |
| [a6] | M. van den Berg, J.-F. Le Gall, "Mean curvature and the heat equation" Math. Z. , 215 (1994) pp. 437–464 |
| [a7] | M. van den Berg, S. Srisatkunarajah, "Heat flow and Brownian motion for a region in 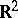 with a polygonal boundary" Probab. Th. Rel. Fields , 86 (1990) pp. 41–52 with a polygonal boundary" Probab. Th. Rel. Fields , 86 (1990) pp. 41–52 |
| [a8] | P. Gilkey, "Heat content asymptotics" Booss (ed.) Wajciechowski (ed.) , Geometric Aspects of Partial Differential Equations , Contemp. Math. , 242 , Amer. Math. Soc. (1999) pp. 125–134 |
| [a9] | D.M. McAvity, "Surface energy from heat content asymptotics" J. Phys. A: Math. Gen. , 26 (1993) pp. 823–830 |
| [a10] | D.M. McAvity, "Heat kernel asymptotics for mixed boundary conditions" Class. Quant. Grav , 9 (1992) pp. 1983–1998 |
| [a11] | A. Savo, "Uniform estimates and the whole asymptotic series of the heat content on manifolds" Geom. Dedicata , 73 (1998) pp. 181–214 |
| [a12] | A. Savo, "Heat content and mean curvature" J. Rend. Mat. Appl. VII Ser. , 18 (1998) pp. 197–219 |
Heat content asymptotics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Heat_content_asymptotics&oldid=49991