Skein module

linear skein

An algebraic object associated to a manifold, usually constructed as a formal linear combination of embedded (or immersed) submanifolds, modulo locally defined relations. In a more restricted setting, a skein module is a module associated to a three-dimensional manifold by considering linear combinations of links in the manifold, modulo properly chosen (skein) relations (cf. also Link; Linear skein). It is the main object of algebraic topology based on knots. In the choice of relations one takes into account several factors:

i) Is the module obtained accessible (computable)?

ii) How precise are the modules in distinguishing three-dimensional manifolds and links in them?

iii) Does the module reflect the topology/geometry of a three-dimensional manifold (e.g. surfaces in a manifold, geometric decomposition of a manifold)?

iv) Does the module admit some additional structure (e.g. filtration, gradation, multiplication, Hopf algebra structure)? One of the simplest skein modules is a 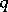-deformation of the first homology group of a three-dimensional manifold 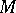, denoted by 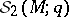. It is based on the skein relation (between non-oriented framed links in )

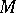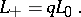Already this simply defined skein module "sees" non-separating surfaces in 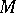. These surfaces are responsible for the torsion part of this skein module.

There is a more general pattern: most of the skein modules analyzed reflect various surfaces in a manifold.

The best studied skein modules use skein relations which worked successfully in classical knot theory (when defining polynomial invariants of links in 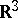, cf. also Link).

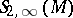1) The Kauffman bracket skein module is based on the Kauffman bracket skein relation , and is denoted by . Among the Jones-type skein modules it is the one best understood. It can be interpreted as a quantization of the coordinate ring of the character variety of 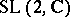representations of the fundamental group of the manifold 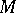, [a4], [a2], [a16]. For 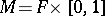, the Kauffman bracket skein module is an algebra (usually non-commutative). It is a finitely-generated algebra for a compact 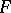[a3], and has no zero divisors [a16]. Incompressible tori and two-dimensional spheres in 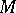yield torsion in the Kauffman bracket skein module; it is a question of fundamental importance whether other surfaces can yield torsion as well.

2) Skein modules based on the Jones–Conway relation (Homflypt relation) are denoted by and generalize skein modules based on the Conway relation which were hinted at by J.H. Conway. For 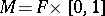, 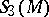is a Hopf algebra (usually neither commutative nor co-commutative), [a19], [a11]. 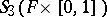is a free module and can be interpreted as a quantization [a6], [a18], [a10], [a19] (cf. also Drinfel'd–Turaev quantization). 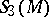is related to the algebraic set of 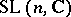representations of the fundamental group of the manifold 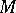, [a17].

3) The skein module based on the Kauffman polynomial relation is denoted by 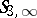and is known to be free for .

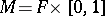4) In homotopy skein modules, 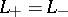for self-crossings. The best studied example is the 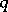-homotopy skein module with the skein relation 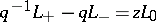for mixed crossings. For 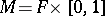it is a quantization, [a7], [a19], [a15], and as noted by U. Kaiser they can be almost completely understood using Lin's singular tori technique [a20].

5) The only studied skein module based on relations deforming -moves to date (2000) is the fourth skein module 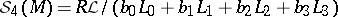, with possible additional framing relation. It is conjectured that in 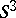this module is generated by trivial links. Motivation for this is the Montesinos–Nakanishi three-move conjecture (cf. Montesinos–Nakanishi conjecture).

6) Extending the family of knots, 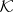, by singular knots, and resolving singular crossing by allows one to define the Vassiliev–Gusarov filtration:

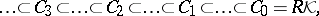where 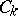is generated by knots with 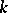singular points. The 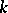th Vassiliev–Gusarov skein module is defined to be a quotient:

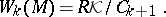The completion of the space of knots with respect to the Vassiliev–Gusarov filtration, 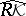, is a Hopf algebra (for 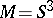). Functions dual to Vassiliev–Gusarov skein modules are called finite type or Vassiliev invariants of knots, [a12].

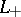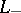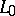Skein modules have their origin in the observation by J.W. Alexander [a1] that his polynomials of three links, , and in 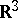, are linearly related. They were envisioned by Conway (linear skein) [a5] and the outline of the theory was given first in the spring of 1987 [a9] after Jones' construction of his polynomial (the Jones polynomial) in 1984; see [a8], [a13], [a14] for the history of the development of skein modules. V.G. Turaev pointed out the importance of skein modules as quantizations, [a19] (cf. also Drinfel'd–Turaev quantization).

References

[a1]	J.W. Alexander, "Topological invariants of knots and links" Trans. Amer. Math. Soc. , 30 (1928) pp. 275–306
[a2]	D. Bullock, C. Frohman, J. Kania–Bartoszyńska, "Understanding the Kauffman bracket skein module" J. Knot Th. Ramifications (1999)
[a3]	D. Bullock, "A finite set of generators for the Kauffman bracket skein algebra" Math. Z. , 231 : 1 (1999) pp. 91–101
[a4]	D. Bullock, "Rings of 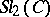-characters and the Kauffman bracket skein module" Comment. Math. Helv. , 72 (1997) pp. 521–542
[a5]	J.H. Conway, "An enumeration of knots and links" J. Leech (ed.) , Computational Problems in Abstract Algebra , Pergamon (1969) pp. 329–358
[a6]	J. Hoste, M. Kidwell, "Dichromatic link invariants" Trans. Amer. Math. Soc. , 321 : 1 (1990) pp. 197–229
[a7]	J. Hoste, J.H. Przytycki, "Homotopy skein modules of oriented 3-manifolds" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 475–488
[a8]	J. Hoste, J.H. Przytycki, "A survey of skein modules of 3-manifolds" A. Kawauchi (ed.) , Knots 90, Proc. Internat. Conf. Knot Theory and Related Topics (Osaka, Japan, August 15-19, 1990) , de Gruyter (1992) pp. 363–379
[a9]	J.H. Przytycki, "Skein modules of 3-manifolds" Bull. Polish Acad. Sci. , 39 : 1–2 (1991) pp. 91–100
[a10]	J.H. Przytycki, "Skein module of links in a handlebody" B. Apanasov (ed.) W.D. Neumann (ed.) A.W. Reid (ed.) L. Siebenmann (ed.) , Topology 90, Proc. Research Sem. Low Dimensional Topology at OSU , de Gruyter (1992) pp. 315–342
[a11]	J.H. Przytycki, "Quantum group of links in a handlebody" M. Gerstenhaber (ed.) J.D. Stasheff (ed.) , Contemporary Math.: Deformation Theory and Quantum Groups with Applications to Mathematical Physics , 134 (1992) pp. 235–245
[a12]	J.H. Przytycki, "Vassiliev–Gusarov skein modules of 3-manifolds and criteria for periodicity of knots" K. Johannson (ed.) , Low-Dimensional Topology (Knoxville, 1992) , Internat. Press, Cambridge, Mass. (1994) pp. 157–176
[a13]	J.H. Przytycki, "Algebraic topology based on knots: an introduction" S. Suzuki (ed.) , Knots 96, Proc. Fifth Internat. Research Inst. MSJ , World Sci. (1997) pp. 279–297
[a14]	J.H. Przytycki, "Fundamentals of Kauffman bracket skein modules" Kobe Math. J. , 16 : 1 (1999) pp. 45–66
[a15]	J.H. Przytycki, "Homotopy and q-homotopy skein modules of 3-manifolds: An example in Algebra Situs" , Proc. Conf. Low-Dimensional Topology in Honor of Joan Birman's 70th Birthday (Columbia Univ./Barnard College, New York, March, 14-15, 1998) (2001)
[a16]	J.H. Przytycki, A.S. Sikora, "On skein algebras and 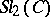-character varieties" Topology , 39 : 1 (2000) pp. 115–148
[a17]	A.S. Sikora, "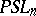-character varieties as spaces of graphs" Trans. Amer. Math. Soc. , 353 (2001) pp. 2773–2804
[a18]	V.G. Turaev, "The Conway and Kauffman modules of the solid torus" J. Soviet Math. , 52 (1990) pp. 2799–2805 Zap. Nauchn. Sem. LOMI , 167 (1988) pp. 79–89
[a19]	V.G. Turaev, "Skein quantization of Poisson algebras of loops on surfaces" Ann. Sci. École Norm. Sup. , 4 : 24 (1991) pp. 635–704
[a20]	V. Kaiser, "Presentations of homotopy skein modules of oriented 3-manifolds" J. Knot Th. Ramifications , 10 : 3 (2001) pp. 461–491