Holomorphy, criteria for

criteria for analyticity

The natural criteria for holomorphy (analyticity) of a 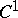(or continuous) function 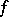in a domain of the complex plane are "infinitesimal" (cf. Analytic function), namely: power series expansions, the Cauchy-Riemann equations, and even the Morera theorem, since it states that

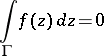for all Jordan curves 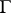such that 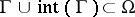, is a necessary and sufficient condition for 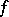being analytic in . The condition (and the usual proofs) depend on the fact that 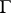can be taken to be arbitrarily small.

The first "non-infinitesimal" condition is due to M. Agranovsky and R.E. Val'skii (see [a2] and [a6] for all relevant references): Let 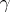be a piecewise smooth Jordan curve, then a function 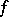continuous in 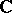is entire (analytic everywhere) if and only if for every transformation 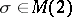and 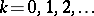it satisfies

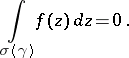(Recall that 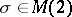means that , , .)

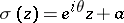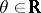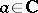A generalization of this theorem and of Morera's theorem which is both local and non-infinitesimal is the following Berenstein–Gay theorem [a3].

Let 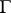be a Jordan polygon contained in 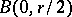and 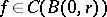; then 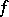is analytic in 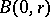if and only if for any 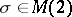such that ,

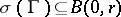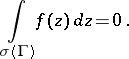This theorem can be extended to several complex variables and other geometries (see [a2], [a5], and [a6] for references).

A different kind of conditions for holomorphy occur when one considers the problem of extending a continuous function defined on a curve in 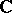(or in a real 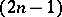-manifold in 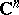) to an analytic function defined in a domain that contains the curve (or hypersurface) on its boundary. This is sometimes called a CR extension. An example of this type, generalizing the moment conditions of the Berenstein–Gay theorem, appears in the work of L. Aizenberg and collaborators (cf. also Analytic continuation into a domain of a function given on part of the boundary; Carleman formulas): Let 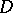be a subdomain of 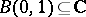, bounded by an arc of the unit circle and a smooth simple curve 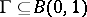and assume that 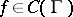. Then there is a function 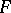, holomorphic inside 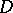and continuous on its closure, such that 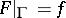if and only if

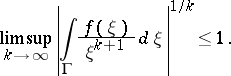A boundary version of the Berenstein–Gay theorem can be proven when regarding the Heisenberg group 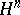(cf. also Nil manifold) as the boundary of the Siegel upper half-space

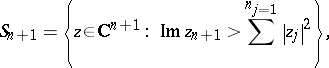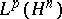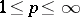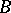but the boundary values are restricted to be in , , [a1]. Related analytic extension theorems from continuous boundary values have been proven by J. Globevnik and E.L. Stout, E. Grinberg, W. Rudin, and others (see [a2] for references) in the bounded "version" of , namely the unit ball of 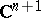, or, more generally, for bounded domains, by essentially considering extensions from the boundary to complex subspaces. An example is the following Globevnik–Stout theorem, [a4].

Let be a bounded domain in 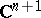with 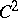boundary. Let 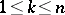and assume 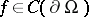is such that

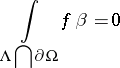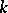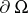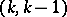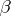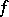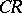for all complex -planes intersecting transversally, and all -forms with constant coefficients. Then is a -function, i.e. has an extension as an analytic function to .

References

[a1]	M. Agranovsky, C. Berenstein, D.C. Chang, "Morera theorem for holomorphic 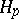functions in the Heisenberg group" J. Reine Angew. Math. , 443 (1993) pp. 49–89
[a2]	C. Berenstein, D.C. Chang, D. Pascuas, L. Zalcman, "Variations on the theorem of Morera" Contemp. Math. , 137 (1992) pp. 63–78
[a3]	C. Berenstein, R. Gay, "Le probléme de Pompeiu local" J. Anal. Math. , 52 (1988) pp. 133–166
[a4]	J. Globevnik, E.L. Stout, "Boundary Morera theorems for holomorphic functions of several complex variables" Duke Math. J. , 64 (1991) pp. 571–615
[a5]	L. Zalcman, "Offbeat integral geometry" Amer. Math. Monthly , 87 (1980) pp. 161–175
[a6]	L. Zalcman, "A bibliographic survey of the Pompeiu problem" B. Fuglede (ed.) et al. (ed.) , Approximation by Solutions of Partial Differential equations , Kluwer Acad. Publ. (1992) pp. 185–194