Pisot sequence

The standard Pisot 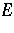-sequence 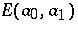is the sequence of positive integers 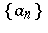defined for 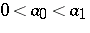by the recursion

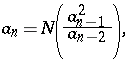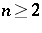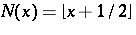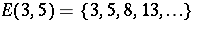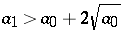if , where denotes the nearest integer function. For example . If , one can show that 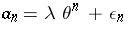, where and 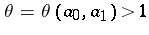and where

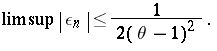Thus, at least when 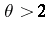, it is clear that 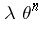is badly distributed modulo (cf. also Distribution modulo one). These sequences were originally considered in [a7] for this reason.

The 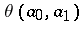are called -numbers. The set of 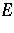-numbers is dense in the interval . contains the set of those for which there is a such that . (Here 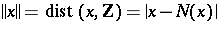denotes the distance from to the nearest integer.) It follows that 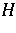is countable. The set also contains the set of Pisot numbers (cf. Pisot number) and the set of Salem numbers (cf. Salem number).

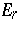The recurrent -sequences are those that satisfy linear recurrence relations. The corresponding subset of is denoted by . It was shown in [a6] that 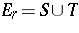. A proof that 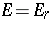, as envisaged in [a7], would show that 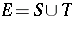and hence that:

i) 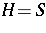; and

ii) is dense in . However, it was proved in [a2] that there are non-recurrent -sequences and that the set of 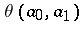corresponding to these is dense in 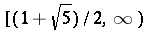. While this does not settle the question of whether 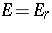(since a given might arise from both a recurrent and a non-recurrent Pisot sequence) it makes this unlikely. The prevailing opinion is that i) is true (Pisot's conjecture), but that ii) is false.

Families of -sequences of the type 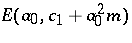were studied in [a5], where conditions are given under which each member of such a family will satisfy a linear recurrence for sufficiently large . In this case the degree of the recurrence does not depend on 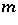. For example, 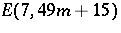is recurrent for 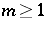[a5] but is non-recurrent for 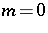[a3].

Many generalizations of Pisot sequences are possible and some were already considered by Ch. Pisot in [a3] (see also [a1], Chapts. 13; 14). One interesting variant replaces the rounding operator 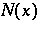by other operators, perhaps dependent on . This can have a dramatic affect on the possible linear recurrence relations satisfied by the sequences (see, e.g. [a4]).

References

[a1]	M.J. Bertin, A. Decomps–Guilloux, M. Grandet–Hugot, M. Pathiaux–Delefosse, J.P. Schreiber, "Pisot and Salem Numbers" , Birkhäuser (1992)
[a2]	D.W. Boyd, "Pisot sequences which satisfy no linear recurrence" Acta Arith. , 32 (1977) pp. 89–98 (See also: vol. 48 (1987), 191-195)
[a3]	D.W. Boyd, "Pisot and Salem numbers in intervals of the real line" Math. Comp. , 32 (1978) pp. 1244–1260
[a4]	D.W. Boyd, "Linear recurrence relations for some generalized Pisot sequences" F.Q. Gouvea (ed.) N. Yui (ed.) , Advances in Number Theory , Oxford Univ. Press (1993) pp. 333–340
[a5]	D.G. Cantor, "On families of Pisot E-sequences" Ann. Sci. Ecole Norm. Sup. , 9 : 4 (1976) pp. 283–308
[a6]	P. Flor, "Über eine Klasse von Folgen naturlicher Zahler" Math. Ann. , 140 (1960) pp. 299–307
[a7]	Ch. Pisot, "La répartition modulo 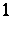et les nombres algébriques" Ann. Scuola Norm. Sup. Pisa Cl. Sci. , 7 : 2 (1938) pp. 205–248