Quasi-symmetric function of a complex variable

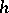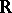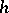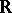An automorphism of the real axis (i.e. a sense-preserving homeomorphism of onto itself) is said to be 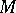-quasi-symmetric on 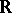(notation: 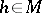-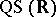) if

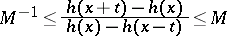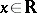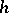holds for all and all . An automorphism of 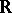is quasi-symmetric (notation: 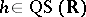) if 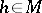- for some 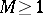. A. Beurling and L.V. Ahlfors established a close relation between 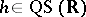and quasi-conformal mappings of the upper half-plane 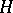onto itself (cf. also Quasi-conformal mapping), cf. statements A), B) below. The term "quasi-symmetric" was proposed in [a2].

A) Any 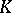-quasi-conformal automorphism 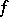of 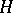normalized by the condition 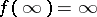admits a homeomorphic extension to the closure of 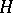and generates in this way 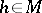-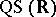, where 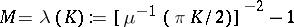, cf. [a1], [a6].

Here 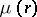, , 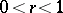is the module of the ring domain 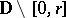, 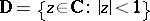(cf. also Modulus of an annulus). The bound for 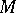is sharp.

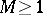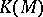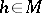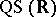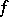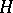B) Conversely, for any there exists a constant such that an arbitrary - has a quasi-conformal extension to with 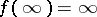whose maximal dilatation 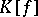satisfies 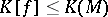, cf. [a1], [a6].

The best value of 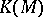known today (2000) is 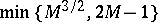, cf. [a5].

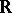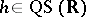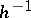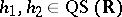Quasi-symmetric functions on satisfy the following: If , so does ; if , so does . However, there exist singular functions on 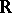that are also quasi-symmetric [a1].

One may also distinguish the class 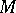- 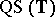of 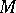-quasi-symmetric automorphisms 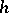of the unit circle 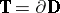. To this end, let 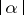denote the length of an open arc 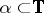. Then 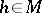- 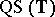if there is an 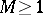such that for any pair 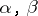of open disjoint subarcs of 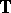with a common end-point

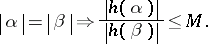The class - 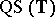has some nice properties: no boundary point of 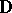is distinguished, Hölder continuity is global on 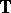and any 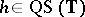may be represented by an absolutely convergent Fourier series, cf. [a3], [a4].

Quasi-symmetric automorphisms of 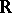or 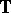are intimately connected with quasi-circles, i.e. image curves of a circle under a quasi-conformal automorphism of 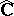. Let 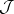be a Jordan curve in the finite plane and let 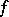(or 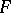) be a conformal mapping of the inside (or outside) domain of 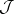onto 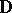(respectively, 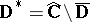). Then 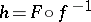is an automorphism of 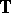and 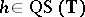is equivalent to 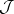being a quasi-circle [a6], [a7].

A sense-preserving homeomorphism 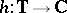is said to be an 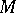-quasi-symmetric function on 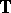(notation: -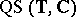) if for any triple , ,

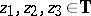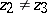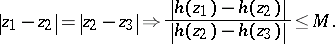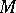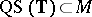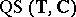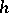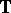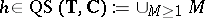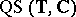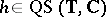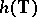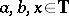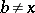Obviously, --. One defines to be a quasi-symmetric function on if -. For any the Jordan curve is a quasi-circle, cf. [a8]. The following characterization of was given by P. Tukia and J. Väisälä in [a9]: For with , put 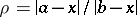. Then 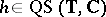if and only if there is an automorphism 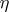of 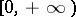such that 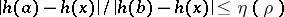for all admissible triples .

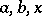References

[a1]	A. Beurling, L.V. Ahlfors, "The boundary correspondence under quasiconformal mappings" Acta Math. , 96 (1956) pp. 125–142
[a2]	J.A. Kelingos, "Contributions to the theory of quasiconformal mappings" , Diss. Univ. Michigan (1963)
[a3]	J.G. Krzyż, "Quasicircles and harmonic measure" Ann. Acad. Sci. Fenn. Ser. A.I. Math. , 12 (1987) pp. 19–24
[a4]	J.G. Krzyż, M. Nowak, "Harmonic automorphisms of the unit disk" J. Comput. Appl. Math. , 105 (1999) pp. 337–346
[a5]	M. Lehtinen, "Remarks on the maximal dilatations of the Beurling–Ahlfors extension" Ann. Acad. Sci. Fenn. Ser. A.I. Math. , 9 (1984) pp. 133–139
[a6]	O. Lehto, K.I. Virtanen, "Quasiconformal mappings in the plane" , Springer (1973)
[a7]	D. Partyka, "A sewing theorem for complementary Jordan domains" Ann. Univ. Mariae Curie–Skłodowska Sect. A , 41 (1987) pp. 99–103
[a8]	Ch. Pommerenke, "Boundary behaviour of conformal maps" , Springer (1992)
[a9]	P. Tukia, J. Väisälä, "Quasisymmetric embeddings of metric spaces" Ann. Acad. Sci. Fenn. Ser. A.I. Math. , 5 (1980) pp. 97–114