Leslie matrix

Matrices arising in a discrete-time deterministic model of population growth [a3]. The Leslie model considers individuals of one sex in a population which is closed to migration. The maximum life span is 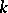time units, and an individual is said to be in the 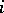th age group if its exact age falls in the interval 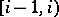, for some 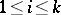. The corresponding Leslie matrix is given by

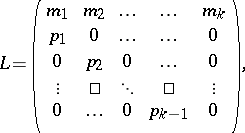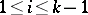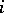where for each , is the proportion of individuals in the th age group who survive one time unit (this is assumed to be positive), and for each 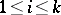, 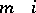is the average number of individuals produced in one time unit by a member of the 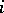th age group. Let 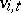be the average number of individuals in the 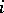th age group at time 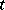units, and let be the vector

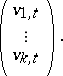Then 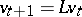, and since the conditions of mortality and fertility are assumed to persist, 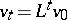for each integer .

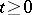If some 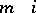is positive, then 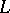has one positive eigen value which is a simple root of the characteristic polynomial. For any eigenvalue of 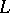, ; indeed has exactly 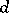eigenvalues of modulus , where 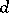is the greatest common divisor of 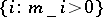. Corresponding to the eigenvalue is the right eigenvector 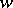given by the formula

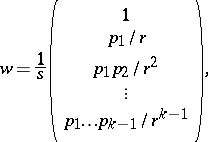where 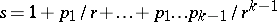. A left eigenvector corresponding to has the form 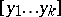, where for ,

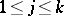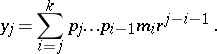The quantity 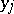is interpreted as the reproductive value of an individual in the 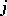th age group.

Suppose that there are indices 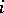, 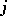such that 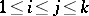, and both 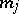and 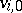are positive. If 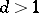, the sequence of age-distribution vectors, 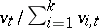, is asymptotically periodic as 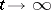, and the period is a divisor of 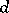depending on 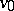. When 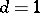, then as 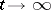, the sequence of age-distribution vectors converges to the eigenvector 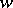, which is called the asymptotic stable age distribution for the population. The nature of the convergence of the age distributions is governed by the quantities 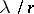, where 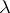is an eigenvalue of 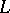distinct from ; a containment region in the complex plane for these quantities has been characterized (cf. [a2], [a5]). The sequence of vectors is asymptotic to 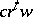, where is a positive constant depending on 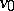; hence is sometimes called the rate of increase for the population. The sensitivity of to changes in 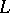is discussed in [a1] and [a6].

Variations on the Leslie model include matrix models for populations classified by criteria other than age (see [a1]), and a model involving a sequence of Leslie matrices changing over time (see [a4] and [a6]). A stochastic version of the Leslie model yields a convergence result for the sequence 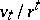under the hypotheses that 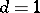and 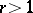(see [a6]).

References

[a1]	H. Caswell, "Matrix population models" , Sinauer (1989)
[a2]	K.P. Hadeler, G. Meinardus, "On the roots of Cauchy polynomials" Linear Alg. & Its Appl. , 38 (1981) pp. 81–102
[a3]	P.H. Leslie, "On the use of matrices in certain population mathematics" Biometrika , 33 (1945) pp. 213–245
[a4]	N. Keyfitz, "Introduction to the mathematics of population" , Addison-Wesley (1977)
[a5]	S. Kirkland, "An eigenvalue region for Leslie matrices" SIAM J. Matrix Anal. Appl. , 13 (1992) pp. 507–529
[a6]	J.H. Pollard, "Mathematical models for the growth of human populations" , Cambridge Univ. Press (1973)