Frobenius matrix
companion matrix
For every polynomial  there are
there are  -matrices
-matrices  such that the characteristic polynomial of
such that the characteristic polynomial of  ,
,  , is equal to
, is equal to  . Indeed, two such are:
. Indeed, two such are:
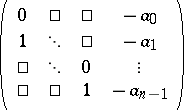 | (a1) |
and
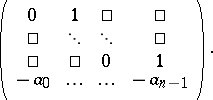 | (a2) |
These two matrices are similar and their minimal polynomial (cf. Minimal polynomial of a matrix) is  , i.e. their similarity invariants are
, i.e. their similarity invariants are 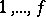 (see Normal form). Both are called the companion matrix, or Frobenius matrix, of
(see Normal form). Both are called the companion matrix, or Frobenius matrix, of 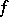 .
.
More generally, a matrix of block-triangular form with as diagonal blocks one of the companion matrices above (all of the same type),
 |
is also sometimes called a Frobenius matrix.
Somewhat related, a matrix with just one column (or one row, but not both) different from the identity matrix is also sometimes called a Frobenius matrix; see, e.g., [a1], p. 169.
For the matrix (a1), the first standard basis vector 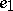 is a cyclic vector (see also Pole assignment problem). The vectors
is a cyclic vector (see also Pole assignment problem). The vectors 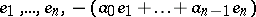 form a so-called Krylov sequence of vectors for
form a so-called Krylov sequence of vectors for 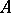 , that is, a sequence of vectors
, that is, a sequence of vectors 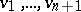 such that
such that 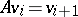 ,
, 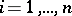 , the
, the  are independent, and
are independent, and 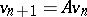 is a linear combination of
is a linear combination of  .
.
The first and second natural canonical forms of a matrix 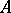 (see also Normal form) are block-diagonal with companion matrices as blocks. Both are also known as the Frobenius normal form of
(see also Normal form) are block-diagonal with companion matrices as blocks. Both are also known as the Frobenius normal form of 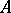 .
.
In a completely different setting, the phrase "Frobenius matrix" refers to a matrix giving the (induced) action of the Frobenius endomorphism of an algebraic variety of characteristic  on, say, the cohomology of that variety.
on, say, the cohomology of that variety.
References
| [a1] | J. Stoer, R. Bulirsch, "Introduction to linear algebra" , Springer (1993) pp. Sect. 6.3 |
| [a2] | M. Marcus, H. Minc, "A survey of matrix theory and matrix inequalities" , Dover (1992) pp. Sect. I.3 |
Frobenius matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frobenius_matrix&oldid=49892