Symmetric channel
A communication channel whose transition function possesses some kind of symmetry. A homogeneous discrete time memoryless channel with finite alphabets 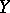 and
and 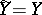 of input and output letters, respectively, and defined by a matrix of transition probabilities
of input and output letters, respectively, and defined by a matrix of transition probabilities  is called a symmetric channel if:
is called a symmetric channel if:
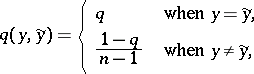 | (*) |
where  is the number of elements of
is the number of elements of  ,
, 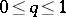 . The most studied example of a memoryless symmetric channel is the binary symmetric channel with matrix of transition probabilities
. The most studied example of a memoryless symmetric channel is the binary symmetric channel with matrix of transition probabilities
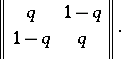 |
For symmetric channels, many important information-theoretic characteristics can either be calculated explicitly or their calculation can be substantially simplified in comparison with non-symmetric channels. For example, for a memoryless symmetric channel with matrix  of the form (*) the capacity
of the form (*) the capacity 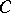 (cf. Transmission rate of a channel) is given by the equation
(cf. Transmission rate of a channel) is given by the equation
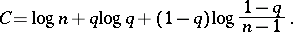 |
For references see ,
cited under Communication channel.
Comments
References
| [a1] | R.C. Gallager, "Information theory and reliable communication" , Wiley (1968) |
Symmetric channel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_channel&oldid=49620