Super-group

Lie super-group

A group object in the category of super-manifolds (cf. Super-manifold). A super-group is defined by a functor from the category of commutative superalgebras into the category of groups. Lie's theorems (cf. Lie theorem) are transferred to super-groups, a fact that gives the correspondence between super-groups and finite-dimensional Lie superalgebras (cf. Superalgebra).

Examples.

1) The super-group 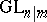is defined by the functor into groups of even invertible matrices from (see Super-space), i.e. of matrices in the form

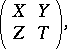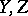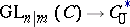where are invertible matrices of orders over , while are matrices over . A homomorphism is defined by the formula

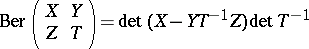(the Berezinian);

2) ;

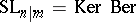3) 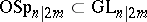and 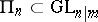; they leave invariant an even, or odd, non-degenerate symmetric bilinear form.

To every super-group 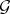and super-subgroup 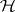of it there is related a super-manifold 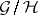, represented by a functor 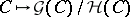. This super-manifold is a homogeneous space of .

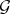References

[1]	Yu.I. Manin, "Gauge fields and complex geometry" , Springer (1988) (Translated from Russian)
[2]	F.A. Berezin, "Introduction to superanalysis" , Reidel (1987) (Translated from Russian)
[3]	D.A. Leites (ed.) , Seminar on supermanifolds , Kluwer (1990)