Stieltjes transform
From Encyclopedia of Mathematics
Revision as of 14:53, 7 June 2020 by Ulf Rehmann (talk | contribs) (Undo revision 48841 by Ulf Rehmann (talk))
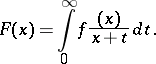 | (*) |
The Stieltjes transform arises in the iteration of the Laplace transform and is also a particular case of a convolution transform.
One of the inversion formulas is as follows: If the function 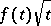 is continuous and bounded on
is continuous and bounded on 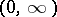 , then
, then
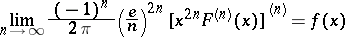 |
for  .
.
The generalized Stieltjes transform is
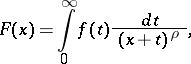 |
where  is a complex number.
is a complex number.
The integrated Stieltjes transform is
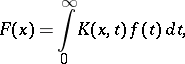 |
where
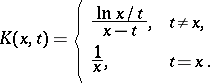 |
Stieltjes transforms are also introduced for generalized functions. The transform (*) was studied by Th.J. Stieltjes (1894–1895).
References
| [1] | D.V. Widder, "The Laplace transform" , Princeton Univ. Press (1972) |
| [2] | R.P. Boas, D.V. Widder, "The iterated Stieltjes transform" Trans. Amer. Math. Soc. , 45 (1939) pp. 1–72 |
| [3] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
| [4] | Y.A. Brychkov, A.P. Prudnikov, "Integral transforms of generalized functions" , Gordon & Breach (1989) (Translated from Russian) |
How to Cite This Entry:
Stieltjes transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stieltjes_transform&oldid=49605
Stieltjes transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stieltjes_transform&oldid=49605
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article