Schur theorems

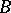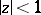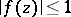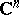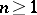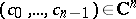Theorems for finding a solution to the coefficient problem for bounded analytic functions. They were obtained by I. Schur [1]. Let be the class of regular functions in satisfying in it the condition . Let , , be the -dimensional complex Euclidean space, its points are -tuples of complex numbers ; let be a set of points such that the numbers are the first coefficients of some function from 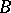. The sets are closed, bounded and convex in 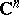. Then the following theorems hold.

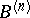Schur's first theorem: To the points on the boundary of there correspond in 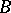only rational functions of the form

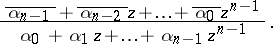Schur's second theorem: A necessary and sufficient condition for 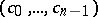to be an interior point of is that the following inequalities hold for :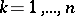

Schur's second theorem provides the complete solution to the coefficient problem for bounded functions in the case of interior points of the coefficients region.

References

[1]	I. Schur, "Ueber Potentzreihen, die im Innern des Einheitkreises berchränkt sind" J. Reine Angew. Math. , 147 (1917) pp. 205–232
[2]	L. Bieberbach, "Lehrbuch der Funktionentheorie" , 2 , Teubner (1931)
[3]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)

References

[a1]	P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11
[a2]	J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) pp. 40