Multiplicative ergodic theorem
Oseledets's multiplicative ergodic theorem, Oseledec's multiplicative ergodic theorem
Consider a linear homogeneous system of differential equations
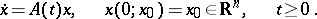 | (a1) |
The Lyapunov exponent of a solution  of (a1) is defined as
of (a1) is defined as
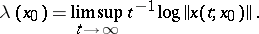 |
A more general setting (Lyapunov exponents for families of system of differential equations) for discussing Lyapunov exponents and related matters is as follows. Let  be a measurable flow on a measure space
be a measurable flow on a measure space 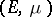 . For all
. For all 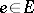 , let
, let 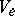 be an
be an  -dimensional vector space. (Think, for example, of a vector bundle
-dimensional vector space. (Think, for example, of a vector bundle 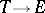 .) A cocycle
.) A cocycle  associated with the flow
associated with the flow 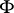 is a measurable function on
is a measurable function on 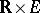 that assigns to
that assigns to 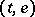 an invertible linear mapping
an invertible linear mapping 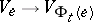 such that
such that
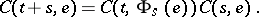 | (a2) |
I.e. if the collection of vector spaces 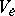 is viewed as an
is viewed as an  -dimensional vector bundle over
-dimensional vector bundle over 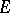 , then
, then 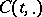 defines an isomorphism of vector bundles
defines an isomorphism of vector bundles 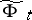 over
over 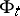 ,
,
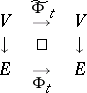 |
and condition (a2) simply says that 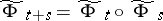 . So
. So 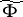 is a flow on
is a flow on  that lifts
that lifts 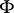 .
. 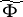 is sometimes called the skew product flow defined by
is sometimes called the skew product flow defined by 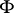 and
and 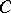 . This set-up is sufficiently general to discuss Lyapunov exponents for non-linear flows, and even stochastic non-linear flows and such things as products of random matrices. If
. This set-up is sufficiently general to discuss Lyapunov exponents for non-linear flows, and even stochastic non-linear flows and such things as products of random matrices. If 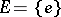 ,
,  , the classical situation (a1) reappears. Let
, the classical situation (a1) reappears. Let 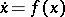 be a differential equation on a manifold
be a differential equation on a manifold 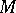 . Take
. Take 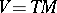 , the tangent bundle over
, the tangent bundle over 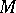 . Let
. Let 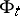 be the flow on
be the flow on 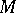 defined by
defined by 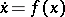 . The associated cocycle is defined by the differential
. The associated cocycle is defined by the differential  of
of 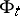 ,
,
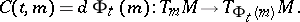 |
For a skew product flow 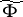 on
on 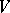 the Lyapunov exponent at
the Lyapunov exponent at 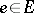 in the direction
in the direction  is defined by
is defined by
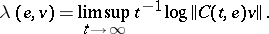 |
The multiplicative ergodic theorem of V.I. Oseledets [a1] now is as follows. Let 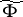 be a skew product flow and assume that there is an invariant probability measure
be a skew product flow and assume that there is an invariant probability measure 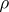 on
on 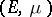 for
for 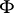 , i.e.
, i.e. 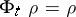 for all
for all 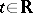 . Suppose, moreover, that
. Suppose, moreover, that
 |
Then there exists a measurable 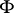 -invariant set
-invariant set 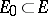 of
of 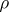 -measure 1 such that for all
-measure 1 such that for all 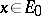 there are
there are 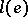 numbers
numbers 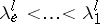 ,
, 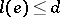 , and corresponding subspaces
, and corresponding subspaces 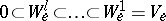 of dimensions
of dimensions 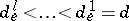 such that for all
such that for all 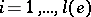 ,
,
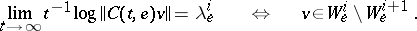 |
If moreover 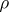 is ergodic for
is ergodic for 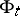 , i.e. all
, i.e. all 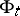 -invariant subsets have
-invariant subsets have 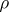 -measure
-measure  or
or 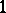 , then the
, then the 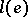 ,
, 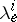 ,
, 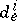 are constants independent of
are constants independent of  (or
(or 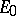 ). However, the spaces
). However, the spaces 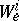 may still depend on
may still depend on 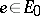 (if the bundle
(if the bundle 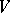 is a trivial bundle so that all the
is a trivial bundle so that all the 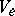 can be identified). The set
can be identified). The set 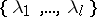 is called the Lyapunov spectrum of the flow. For more details and applications cf. [a2], [a3].
is called the Lyapunov spectrum of the flow. For more details and applications cf. [a2], [a3].
References
| [a1] | V.I. [V.I. Oseledets] Oseledec, "A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems" Trans. Moscow Math. Soc. , 19 (1968) pp. 197–231 Trudy Moskov. Mat. Obshch. , 19 (1968) pp. 179–210 |
| [a2] | W. Kliemann, "Analysis of nonlinear stochastic systems" W. Schiehlen (ed.) W. Wedig (ed.) , Analysis and estimation of stochastic mechanical systems , Springer (Wien) (1988) pp. 43–102 |
| [a3] | L. Arnold (ed.) V. Wihstutz (ed.) , Lyapunov exponents , Lect. notes in math. , 1186 , Springer (1986) |
Multiplicative ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplicative_ergodic_theorem&oldid=49322