Zygmund class of functions
Let 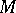 be a positive real number. The Zygmund class
be a positive real number. The Zygmund class 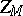 is the class of continuous
is the class of continuous 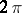 -periodic functions
-periodic functions  with the property that for all
with the property that for all  and all
and all  the inequality
the inequality
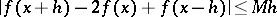 |
holds. The class  was introduced by A. Zygmund [1]. In terms of this class one can obtain a conclusive solution to the Jackson–Bernstein problem on direct and inverse theorems in the theory of approximation of functions (cf. Bernstein theorem; Jackson theorem). For example: A continuous
was introduced by A. Zygmund [1]. In terms of this class one can obtain a conclusive solution to the Jackson–Bernstein problem on direct and inverse theorems in the theory of approximation of functions (cf. Bernstein theorem; Jackson theorem). For example: A continuous 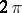 -periodic function
-periodic function 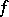 belongs to the Zygmund class
belongs to the Zygmund class 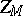 for some
for some 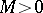 if and only if its best uniform approximation error
if and only if its best uniform approximation error  by trigonometric polynomials of degree
by trigonometric polynomials of degree 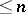 satisfies the inequality
satisfies the inequality
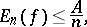 |
where  is a constant. The modulus of continuity
is a constant. The modulus of continuity  of any function
of any function 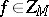 admits the estimate
admits the estimate
 |
in which the constant  cannot be improved on for the entire class
cannot be improved on for the entire class  [3].
[3].
References
| [1] | A. Zygmund, "Smooth functions" Duke Math. J. , 12 : 1 (1945) pp. 47–76 ((Also: Selected papers of Antoni Zygmund, Vol. 2, Kluwer, 1989, pp. 184–213.)) |
| [2] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [3] | A.V. Efimov, "Estimation of the modules of continuity of functions of class 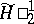 " Izv. Akad. Nauk. SSSR Ser. Mat. , 21 : 2 (1957) pp. 283–288 (In Russian) " Izv. Akad. Nauk. SSSR Ser. Mat. , 21 : 2 (1957) pp. 283–288 (In Russian) |
Comments
The quantity
 |
for a 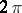 -periodic function
-periodic function  , is its Zygmund modulus. In terms of this, Zygmund's theorem above can also be stated as: A
, is its Zygmund modulus. In terms of this, Zygmund's theorem above can also be stated as: A 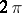 -periodic function
-periodic function  satisfies
satisfies  for some
for some  if and only if
if and only if  (
( ) for some
) for some 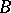 .
.
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) pp. 203ff |
Zygmund class of functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zygmund_class_of_functions&oldid=49251