Zhegalkin algebra
The special algebra 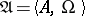 , where
, where
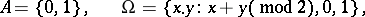 |
and 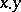 is the multiplication operation. The clone
is the multiplication operation. The clone  of the action of
of the action of  on
on 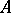 is of interest. Every operation in
is of interest. Every operation in 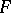 is a polynomial
is a polynomial 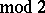 , a so-called Zhegalkin polynomial, named after I.I. Zhegalkin, who initiated the investigation of this clone [1]. He proved that every finitary operation on
, a so-called Zhegalkin polynomial, named after I.I. Zhegalkin, who initiated the investigation of this clone [1]. He proved that every finitary operation on 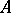 is contained in
is contained in 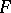 . Thus, the study of properties of
. Thus, the study of properties of 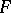 includes, in particular, the study of all algebras
includes, in particular, the study of all algebras  for arbitrary
for arbitrary 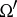 .
.
References
| [1] | I.I. Zhegalkin, Mat. Sb. , 34 : 1 (1927) pp. 9–28 |
| [2] | P.M. Cohn, "Universal algebra" , Reidel (1986) |
| [3] | S.V. Yablonskii, G.P. Gavrilov, V.B. Kudryavtsev, "Functions of the algebra of logic and Post classes" , Moscow (1966) (In Russian) |
Comments
In other words, the Zhegalkin algebra is the two-element Boolean ring, the field 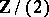 or the free Boolean algebra on
or the free Boolean algebra on  generators. As such, it is generally not given a distinctive name in the Western literature. Cf. e.g. Boolean algebra; Boolean equation. The study of all algebras
generators. As such, it is generally not given a distinctive name in the Western literature. Cf. e.g. Boolean algebra; Boolean equation. The study of all algebras  is the subject of E.L. Post's dissertation [a1].
is the subject of E.L. Post's dissertation [a1].
References
| [a1] | E.L. Post, "Two-valued iterative systems of mathematical logic" , Princeton Univ. Press (1941) |
Zhegalkin algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zhegalkin_algebra&oldid=49249