Let 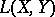 be the (graded) free Lie algebra on two generators over
be the (graded) free Lie algebra on two generators over 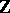 ,
,  the graded free associative algebra on two generators over
the graded free associative algebra on two generators over 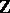 and
and  its completion with respect to the augmentation ideal (where both
its completion with respect to the augmentation ideal (where both  and
and 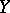 have degree
have degree 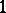 ). For each
). For each  without constant term, let
without constant term, let 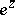 denote the element
denote the element
of  . Then there exist elements
. Then there exist elements 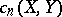 , homogeneous of degree
, homogeneous of degree  , and
, and 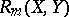 , homogeneous of degree
, homogeneous of degree 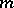 in
in  and of degree
and of degree  in
in 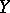 , in
, in  which are Lie elements, i.e. they are in
which are Lie elements, i.e. they are in 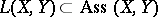 , and which are such that
, and which are such that
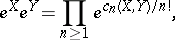 | (a1) |
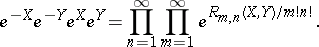 | (a2) |
Here the factors on the right-hand side are to be taken in the natural order for (a1), while in the case of (a2) the product is first taken over  and then over
and then over  . The
. The 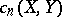 are recursively defined by:
are recursively defined by:
These formulas find application in (combinatorial) group theory, algebraic topology and quantum theory, cf., e.g., [a2]–[a4]. For convergence results (for  and
and 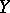 elements of a Banach algebra) concerning formula (a1) and for more general formulas cf., e.g., [a2].
elements of a Banach algebra) concerning formula (a1) and for more general formulas cf., e.g., [a2].
References
| [a1] | H. Zassenhaus, "Über Lie'schen Ringe mit Primzahlcharakteristik" Abh. Math. Sem. Univ. Hamburg , 13 (1940) pp. 1–100 |
| [a2] | M. Suzuki, "On the convergence of exponential operators - the Zassenhaus formula, BCH formula and systematic approximants" Comm. Math. Phys. , 57 (1977) pp. 193–200 |
| [a3] | W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations in terms of generators and relations" , Wiley (Interscience) (1966) pp. 412 |
| [a4] | H.J. Baues, "Commutator calculus and groups of homotopy classes" , Cambridge Univ. Press (1981) |
How to Cite This Entry:
Zassenhaus formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zassenhaus_formula&oldid=49246
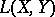 be the (graded) free Lie algebra on two generators over
be the (graded) free Lie algebra on two generators over 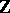 ,
,  the graded free associative algebra on two generators over
the graded free associative algebra on two generators over 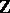 and
and  its completion with respect to the augmentation ideal (where both
its completion with respect to the augmentation ideal (where both  and
and 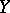 have degree
have degree 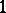 ). For each
). For each  without constant term, let
without constant term, let 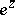 denote the element
denote the element
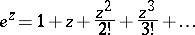
 . Then there exist elements
. Then there exist elements 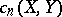 , homogeneous of degree
, homogeneous of degree  , and
, and 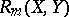 , homogeneous of degree
, homogeneous of degree 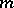 in
in  and of degree
and of degree  in
in 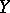 , in
, in  which are Lie elements, i.e. they are in
which are Lie elements, i.e. they are in 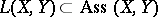 , and which are such that
, and which are such that
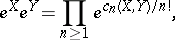
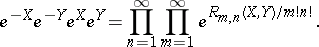
 and then over
and then over  . The
. The 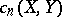 are recursively defined by:
are recursively defined by:

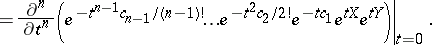
 and
and 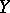 elements of a Banach algebra) concerning formula (a1) and for more general formulas cf., e.g., [a2].
elements of a Banach algebra) concerning formula (a1) and for more general formulas cf., e.g., [a2].