Wurf
An ordered set of 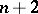 points in an
points in an  -dimensional projective space if
-dimensional projective space if 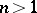 , and of four points if
, and of four points if 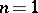 . If
. If 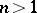 , no
, no 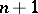 points of the wurf belong to a hyperplane. Two wurfs on a straight line or on a conical section will be equal if the two quadruplets of points of which they are constituted are projective. The operations of addition and multiplication can be defined for wurfs. In so doing it is expedient to use wurfs with three base points
points of the wurf belong to a hyperplane. Two wurfs on a straight line or on a conical section will be equal if the two quadruplets of points of which they are constituted are projective. The operations of addition and multiplication can be defined for wurfs. In so doing it is expedient to use wurfs with three base points 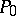 ,
, 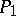 ,
, 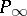 — the so-called reduced wurfs. In this manner operations over wurfs are reduced to operations over points.
— the so-called reduced wurfs. In this manner operations over wurfs are reduced to operations over points.
The sum of two points 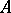 and
and 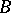 (other than
(other than 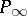 ) is the point
) is the point 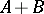 which corresponds to
which corresponds to 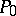 under the hyperbolic involution
under the hyperbolic involution 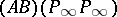 that interchanges
that interchanges 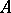 and
and  and leaves
and leaves 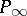 fixed. The operation of addition is both commutative and associative. The point
fixed. The operation of addition is both commutative and associative. The point 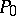 is the zero element, and to each point
is the zero element, and to each point 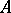 there corresponds an opposite point
there corresponds an opposite point 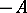 :
: 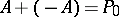 .
.
The product of two points 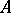 and
and 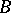 other than
other than 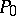 ,
, 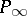 is the point
is the point 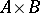 which, together with
which, together with 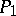 , forms a pair under the elliptic or hyperbolic involution
, forms a pair under the elliptic or hyperbolic involution 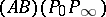 that interchanges
that interchanges 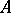 with
with 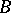 and
and 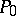 with
with 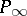 . The operation of multiplication is both commutative and associative. The point
. The operation of multiplication is both commutative and associative. The point 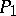 is the unit element, and for each point
is the unit element, and for each point 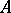 there exists an inverse point
there exists an inverse point 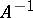 :
: 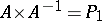 .
.
References
| [1] | K.G.C. von Staudt, "Beiträge zur Geometrie der Lage" , 2 , Korn , Nürnberg (1959) pp. 166–194 |
| [2] | H.S.M. Coxeter, "The real projective plane" , Springer (1992) pp. Chapt. 11 |
Comments
K. von Staudt used his "Würfe" for the coordinatization of projective geometry. Nowadays his methods are considered obsolete, although ingenious.
The modern methods began with [a1].
If 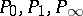 are the points on the projective line with coordinates
are the points on the projective line with coordinates 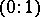 ,
, 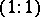 ,
, 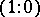 , respectively, and
, respectively, and 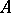 and
and 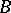 are the points with coordinates
are the points with coordinates 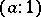 and
and 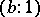 , then the sum and product of the wurf equivalence classes
, then the sum and product of the wurf equivalence classes 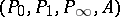 and
and 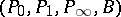 are the wurf equivalence classes
are the wurf equivalence classes 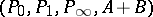 and
and  , where
, where 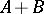 and
and 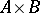 have the coordinates
have the coordinates 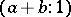 and
and 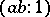 .
.
References
| [a1] | O. Veblen, J.W. Young, "Projective geometry" , 1–2 , Blaisdell (1946) |
Wurf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wurf&oldid=49237