Wirsing theorems

Multiplicative arithmetic functions 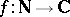are determined by their values at the prime powers (cf. Multiplicative arithmetic function). Higher prime powers 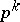, , 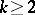are rare, and so the behaviour of 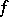at the primes should strongly influence the behaviour of 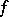in general. This vague idea, which also lies behind the theorems of Delange and Elliott (see Delange theorem; Elliott–Daboussi theorem), led E. Wirsing in 1961 [a6] to the following result, which provides asymptotic formulas for a large class of non-negative multiplicative functions.

Let 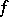be a non-negative multiplicative function. Assume that the values of 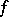at the primes satisfy, with some positive constant ,

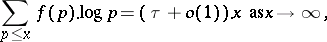(a1)

and that the values of 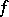at higher prime powers are not "too large" :

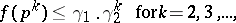where 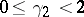. Then

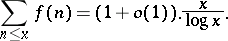(a2)

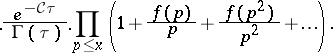The proof uses an inversion of the order of summation in 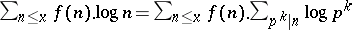, to show that

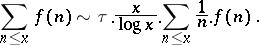The last sum may be dealt with by elementary arguments or by a skilful application of the Hardy–Littlewood–Karamata Tauberian theorem (cf. Tauberian theorems).

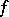In 1967, B.V. Levin and A.S. Fainleib [a5] also gave asymptotic evaluations of sums for multiplicative functions , by reducing the problem to the study of the asymptotic behaviour of solutions of integral equations of the form .

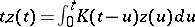In [a6], Wirsing also deduced results for complex-valued multiplicative functions. Unfortunately, these results did not contain the prime number theorem (in the form 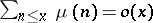; cf. also de la Vallée-Poussin theorem), and they did not settle the Erdös–Wintner conjecture: Any multiplicative function assuming only the values and 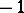has a mean value (see [a1]).

But six years later, in 1967 [a7], Wirsing was able to settle this conjecture. He proved in an elementary, but complicated, way several results on multiplicative functions. For example: If 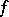is a real-valued multiplicative function and if 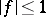, then the mean value 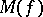exists [a7], Satz 1.2.2.

The asymptotic formula (a2) can now be proved under the condition

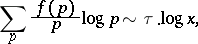which is much weaker than (a1). However, 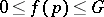and some other restrictions must be assumed. There are also corresponding, complicated, results on complex-valued multiplicative functions, [a7], Satz 1.2.

In 1968, G. Halász [a2] gave a more satisfactory result (see Halász mean value theorem). In 1986, A. Hildebrand [a4] proved a Wirsing-type theorem by elementary means (his result also contains a proof of the Erdös–Wintner conjecture): There exists a universal constant 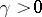with the property that for any multiplicative function 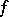with values in the interval 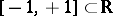and with divergent series , the estimate

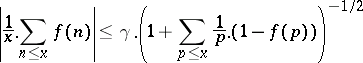holds for any . As shown in [a3], it is possible to deduce stronger estimates by analytical methods.

References

[a1]	P. Erdös, "Some unsolved problems" Michigan Math. J. , 4 (1957) pp. 291–300
[a2]	G. Halász, "Über die Mittelwerte multiplikativer zahlentheoretischer Funktionen" Acta Math. Acad. Sci. Hung. , 19 (1968) pp. 365–403
[a3]	G. Halász, "On the distribution of additive and the mean values of multiplicative arithmetic functions" Studia Sci. Math. Hung. , 6 (1971) pp. 211–233
[a4]	A. Hildebrand, "On Wirsing's mean value theorem for multiplicative functions" Bull. London Math. Soc. , 18 (1986) pp. 147–152
[a5]	B.V. Levin, A.S. Fainleib, "Application of certain integral equations to questions of the theory of numbers" Uspekhi Mat. Nauk , 22 : 3 (135) (1967) pp. 119–197 (In Russian)
[a6]	E. Wirsing, "Das asymptotische Verhalten von Summen über multiplikative Funktionen" Math. Ann. , 143 (1961) pp. 75–102
[a7]	E. Wirsing, "Das asymptotische Verhalten von Summen über multiplikative Funktionen, II" Acta Math. Acad. Sci. Hung. , 18 (1967) pp. 411–467