Wiener measure(2)
The probability distribution of a Brownian motion 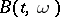 ,
, 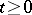 ,
, 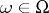 , where
, where 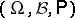 is a probability space. The Wiener measure is denoted by
is a probability space. The Wiener measure is denoted by 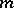 or
or 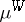 . Brownian motion
. Brownian motion 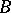 is a Gaussian process such that
is a Gaussian process such that
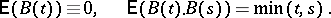 |
Given a Brownian motion 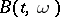 , one can form a new Brownian motion
, one can form a new Brownian motion 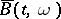 satisfying:
satisfying:
i) 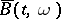 is continuous in
is continuous in  for almost all
for almost all 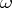 .
.
ii)  for every
for every 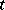 .
.
Such a process 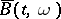 is called a continuous version of
is called a continuous version of 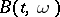 .
.
The Kolmogorov–Prokhorov theorem tells that the probability distribution 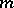 of the Brownian motion
of the Brownian motion 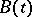 can be introduced in the space
can be introduced in the space 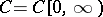 of all continuous functions on
of all continuous functions on 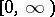 .
.
Let 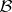 be the topological Borel field (cf. also Borel field of sets) of subsets of
be the topological Borel field (cf. also Borel field of sets) of subsets of 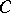 . The measure space
. The measure space 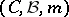 thus obtained is the Wiener measure space.
thus obtained is the Wiener measure space.
The integral of a 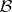 -measurable functional on
-measurable functional on 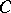 with respect to
with respect to 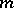 is defined in the usual manner. (See also Stochastic integral.)
is defined in the usual manner. (See also Stochastic integral.)
An elementary and important example of a 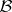 -measurable functional of
-measurable functional of 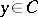 is a stochastic bilinear form, given by
is a stochastic bilinear form, given by 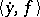 , where
, where 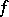 is an
is an 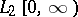 -function. It is usually denoted by
-function. It is usually denoted by 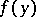 . It is, in fact, defined by
. It is, in fact, defined by 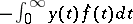 for smooth functions
for smooth functions 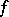 . For a general
. For a general 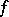 ,
, 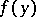 can be approximated by stochastic bilinear forms defined by smooth functions
can be approximated by stochastic bilinear forms defined by smooth functions 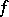 . An integral of this type is called a Wiener integral. Under certain restrictions, such as non-anticipation, the integral can be extended to the case where the integrand is a functional of
. An integral of this type is called a Wiener integral. Under certain restrictions, such as non-anticipation, the integral can be extended to the case where the integrand is a functional of 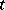 and
and 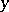 . And an even more general case has been proposed.
. And an even more general case has been proposed.
The class of general (non-linear) functionals of 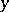 is introduced as follows. Let
is introduced as follows. Let 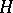 be the Hilbert space of all complex-valued, square-
be the Hilbert space of all complex-valued, square- -integrable functionals on
-integrable functionals on 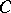 . Then,
. Then, 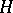 admits a direct sum decomposition (Fock space)
admits a direct sum decomposition (Fock space)
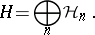 |
The subspace 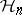 is spanned by the Fourier–Hermite polynomials of degree
is spanned by the Fourier–Hermite polynomials of degree  , which are of the form
, which are of the form
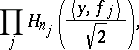 |
where  and
and 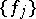 is a complete orthonormal system in the Hilbert space
is a complete orthonormal system in the Hilbert space 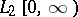 . The space
. The space 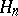 can be interpreted as the space of multiple Wiener integrals of degree
can be interpreted as the space of multiple Wiener integrals of degree  , due to K. Itô.
, due to K. Itô.
References
| [a1] | R. Cameron, W.T. Martin, "The orthogonal development of non-linear functionals in series of Fourier–Hermite functionals" Ann. of Math. (2) , 48 pp. 385–392 |
| [a2] | T. Hida, "Brownian motion" , Applications of Mathematics , 11 , Springer (1980) |
Wiener measure(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener_measure(2)&oldid=49221