Wiener integral

An abstract integral of Lebesgue type over sets in an infinite-dimensional function space of functionals defined on these sets. Introduced by N. Wiener in the nineteentwenties in connection with problems on Brownian motion [1], [2].

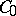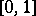Let be the vector space of continuous real-valued functions defined on such that 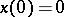, with norm

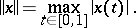The set

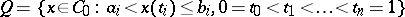is called a quasi-interval of this space. Here, 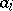and 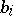may be equal to 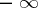and 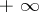, respectively, but then the symbol 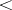must replace 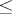. The whole space 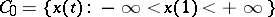is an example of a quasi-interval.

The Wiener measure of a quasi-interval 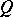is the number

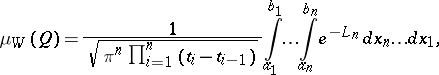where

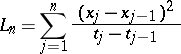and 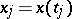. This measure extends to a 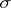-additive measure on the Borel field of sets generated by the quasi-intervals, known also as Wiener measure.

Let 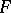be a functional defined on 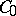that is measurable with respect to the measure 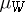. The Lebesgue-type integral

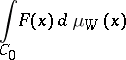is known as the Wiener integral, or as the integral with respect to the Wiener measure, of the functional 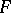. If 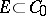is measurable, then

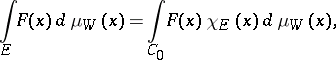where 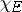is the characteristic function of the set .

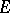Wiener's integral displays several properties of the ordinary Lebesgue integral. In particular, a functional which is bounded and measurable on a set 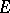is integrable with respect to the Wiener measure on this set and if, in addition, the functional 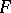is continuous and non-negative, then

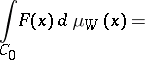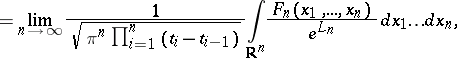where 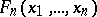is the value of 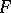at linear interpolation of 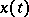between points .

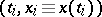The computation of a Wiener integral presents considerable difficulties, even for the simplest functionals. The task may sometimes be reduced to solving a single differential equation [1].

There is a method by which Wiener's integral may be approximately computed through approximating it by finite-dimensional Stieltjes integrals of a high multiplicity (cf. Stieltjes integral).

References

[1]	I.M. Koval'chik, "The Wiener integral" Russian Math. Surveys , 18 : 1 (1963) pp. 97–134 Uspekhi Mat. Nauk , 18 : 1 (1963) pp. 97–134
[2]	G.E. Shilov, "Integration in infinite dimensional spaces and the Wiener integral" Russ. Math. Surveys , 18 : 2 (1963) pp. 99–120 Uspekhi Mat. Nauk , 2 (1963) pp. 99–120

Comments

Further references on the computation of Wiener integrals in the sense described above are [a1] and [a2]. In the Western literature, the term "Wiener integral" normally refers to the stochastic integral of a deterministic function 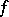such that 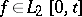for each 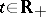, with respect to the Wiener process 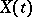defined on a probability space 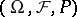. This is denoted by

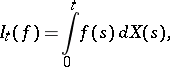and is defined as follows. If 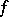is a simple function, i.e. 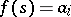for 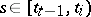, where 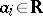and 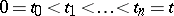, then

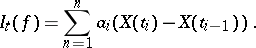Let 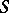denote the set of simple functions. For 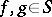, a computation shows that 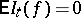, , 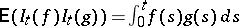i.e. 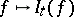is an inner-product preserving mapping from 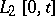to 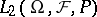. For any 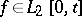there exists a sequence 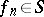such that 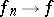. 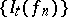is then a Cauchy sequence in 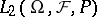, and one defines

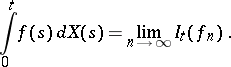Notable features of this construction are as follows.

It is possible to define 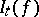simultaneously for all 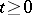and to obtain a version which is a Gaussian martingale with continuous sample paths

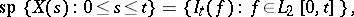where "sp" denotes the closed linear span in 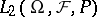. Information on the Wiener integral in this sense is given in [a3], [a4].

References

[a1]	A.J. Chorin, "Accurate evaluation of Wiener integrals" Math. Comp. , 27 (1973) pp. 1–15
[a2]	G.L. Blankenschip, J.S. Baras, "Accurate evaluation of stochastic Wiener integrals with applications to scattering in random media and to nonlinear filtering" SIAM J. Appl. Math. , 41 (1981) pp. 518–552
[a3]	M.H.A. Davis, "Linear estimation and stochastic control" , Chapman & Hall (1977)
[a4]	R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , I , Springer (1977) (Translated from Russian)
[a5]	J. Yeh, "Stochastic processes and the Wiener integral" , M. Dekker (1973)
[a6]	B. Simon, "Functional integration and quantum physics" , Acad. Press (1979) pp. 4–6
[a7]	L.C.G. Rogers, D. Williams, "Diffusions, Markov processes, and martingales" , 2. Itô calculus , Wiley (1987)
[a8]	H. Bauer, "Probability theory and elements of measure theory" , Holt, Rinehart & Winston (1972) pp. Chapt. 11 (Translated from German)