Wiener chaos decomposition
Let 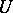 be a dense subspace of a separable Hilbert space
be a dense subspace of a separable Hilbert space 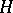 . The triplet
. The triplet 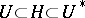 given by the injection
given by the injection 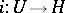 is obtained by identifying
is obtained by identifying 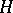 with its dual, taking the dual of
with its dual, taking the dual of 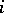 , and endowing
, and endowing 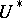 , the algebraic dual of
, the algebraic dual of 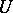 , with the weak topology. For any real
, with the weak topology. For any real 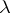 , let
, let  be the Hilbert space obtained from
be the Hilbert space obtained from 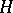 by multiplying the norm on
by multiplying the norm on  by
by  .
.
The dual of the symmetric 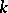 -fold tensor product
-fold tensor product 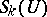 is the space
is the space  of all homogeneous polynomials of degree
of all homogeneous polynomials of degree 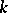 on
on 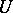 . The value of
. The value of  at
at 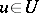 is
is 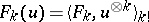 . Thus, for each
. Thus, for each 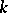 there is a triplet
there is a triplet
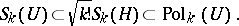 | (a1) |
Taking the direct sum of the internal space 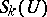 and the Hilbert sum of the central spaces there results a triplet
and the Hilbert sum of the central spaces there results a triplet
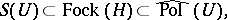 | (a2) |
called dressed Fock space. The middle term is the usual Fock space
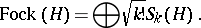 | (a3) |
The external space is the space 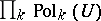 of all formal power series on
of all formal power series on 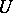 . The value
. The value 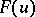 at
at 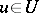 of such an
of such an 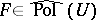 is defined as
is defined as 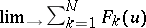 , if this limit exists. For example, for any
, if this limit exists. For example, for any 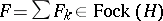 one has
one has
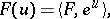 | (a4) |
where  .
.
A probabilized vector space is a structure
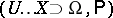 | (a5) |
where 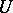 and
and 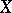 are two spaces in duality and
are two spaces in duality and 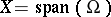 is linearly generated by the subset
is linearly generated by the subset  of
of 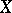 . This subset is endowed with a Polish (or Suslin) topology such that any
. This subset is endowed with a Polish (or Suslin) topology such that any 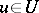 defines a Borel function
defines a Borel function  on
on  . The space
. The space 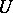 contains a countable subset separating the points of
contains a countable subset separating the points of  (so that the Borel
(so that the Borel 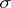 -field is generated by
-field is generated by 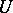 ). Finally,
). Finally, 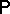 is a probability measure on this
is a probability measure on this 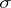 -field.
-field.
Assume, moreover, that the space of cylindrical polynomials 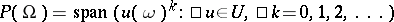 is dense in
is dense in 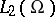 . Assume that the following bilinear form on
. Assume that the following bilinear form on 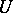 is a scalar product:
is a scalar product:
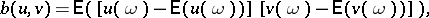 | (a6) |
and let 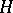 be the completion of
be the completion of 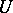 . For any
. For any 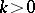 , let
, let  denote the orthogonal projection of
denote the orthogonal projection of 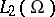 with range
with range 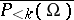 , the closure of
, the closure of 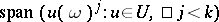 . Let
. Let  be the orthogonal complement of
be the orthogonal complement of 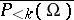 in
in  . This space is called the
. This space is called the 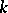 -th homogeneous chaos. The space
-th homogeneous chaos. The space 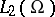 is the Hilbert direct sum of the
is the Hilbert direct sum of the 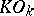 . One says that
. One says that 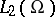 admits a decomposition in chaos if for any
admits a decomposition in chaos if for any 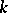 the following mapping is isometric:
the following mapping is isometric:
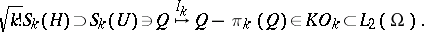 |
The collection of these isometries for 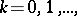 is an isometry
is an isometry 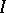 whose inverse
whose inverse
 | (a7) |
extended to distributions on  , is the starting point of distribution calculus on
, is the starting point of distribution calculus on  . Because of (a4),
. Because of (a4), 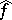 is explicitly given by
is explicitly given by
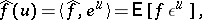 | (a8) |
where  .
.
Decomposition in chaos was discovered by N. Wiener (in the case  is Wiener space), [a1]. Further contributions are due to Th.A. Dwyer and I. Segal ([a2], [a3]) and these have been important for constructive quantum field theory. K. Itô obtained a decomposition into chaos for Poisson probability spaces and interpreted
is Wiener space), [a1]. Further contributions are due to Th.A. Dwyer and I. Segal ([a2], [a3]) and these have been important for constructive quantum field theory. K. Itô obtained a decomposition into chaos for Poisson probability spaces and interpreted 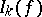 as iterated stochastic integrals. For formula (a8), extended to distributions for Gaussian probability spaces, cf. [a5], [a6], [a7], [a9], [a10]. There are links with Malliavin calculus, [a8].
as iterated stochastic integrals. For formula (a8), extended to distributions for Gaussian probability spaces, cf. [a5], [a6], [a7], [a9], [a10]. There are links with Malliavin calculus, [a8].
For more material cf. e.g. also [a11], [a12]; Wick product and White noise analysis, and the references therein.
References
| [a1] | N. Wiener, "The homogeneous chaos" Amer. J. Math. , 60 (1938) pp. 897–936 |
| [a2] | Th.A., III Dwyer, "Partial differential equations in Fischer–Fock spaces for the Hilbert–Schmidt holomorphy type" Bull. Amer. Math. Soc. , 77 (1971) pp. 725–730 |
| [a3] | I. Segal, "Tensor algebras over Hilbert spaces, I" Trans. Amer. Math. Soc. , 81 (1956) pp. 106–134 |
| [a4] | K. Itô, "Multiple Wiener integral" J. Math. Soc. Japan (1951) pp. 157–169 |
| [a5] | P. Krée, "Solutions faibles d'equations aux dérivées fonctionelles II" , Sem. P. Lelong 1973/1974 , Lect. notes in math. , 474 , Springer (1974) pp. 16–47 |
| [a6] | P. Krée, R. Raczka, "Kernels and symbols of operators in quantum field theory" Ann. Inst. H. Poincaré (1978) |
| [a7] | B. Lascar, "Propriétés locales des espaces de type Sobolev en dimension infinie" Comm. Partial Diff. Eq. , 1 : 6 (1976) pp. 561–584 |
| [a8] | D. Ocone, "Malliavin calculus and stochastic integral representation of functionals of diffusion processes" Stochastics , 12 (1984) pp. 161–185 |
| [a9] | M. Krée, "Propriété de trace en dimension infinie d'espaces du type Sobolev" C.R Acad. Sci. Paris , 279 (1974) pp. 157–160 |
| [a10] | M. Krée, "Propriété de trace en dimension infinie d'espaces de type Sobolev" Bull. Soc. Math. de France , 105 (1977) pp. 141–163 |
| [a11] | G. Kallianpur, "The role of reproducing kernel Hilbert spaces in the study of Gaussian processes" P. Ney (ed.) , Advances in probability and related topics , 2 , M. Dekker (1970) pp. 49–84 |
| [a12] | J. Neveu, "Processus aléatoires Gaussiens" , Univ. Montréal (1968) |
Wiener chaos decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener_chaos_decomposition&oldid=49218