Whittaker functions

The functions and which are solutions of the Whittaker equation

(*)

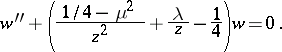The function satisfies the equation

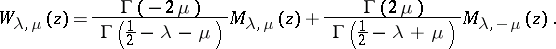The pairs of functions and are linearly independent solutions of the equation (*). The point is a branching point for , and is an essential singularity.

Relation with other functions:

with the degenerate hypergeometric function:

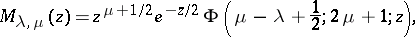with the modified Bessel functions and the Macdonald function:

with the probability integral:

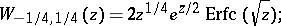with the Laguerre polynomials:

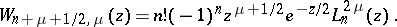References

[1]	H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953)
[2]	E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952)

Comments

The Whittaker function 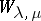can be expressed in terms of the 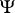-function introduced in confluent hypergeometric function:

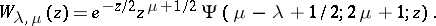Thus, the special cases discussed in confluent hypergeometric function can be rewritten as special cases for the Whittaker functions. See also the references given there.