Whitehead torsion
An element of the reduced Whitehead group 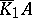 , constructed from a complex of
, constructed from a complex of 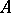 -modules. In particular, one has the Whitehead torsion of a mapping complex. Let
-modules. In particular, one has the Whitehead torsion of a mapping complex. Let  be a ring and let
be a ring and let 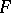 be a finitely-generated free
be a finitely-generated free 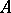 -module. Given two bases
-module. Given two bases 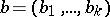 and
and 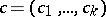 of
of  , if
, if 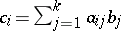 , then the matrix
, then the matrix 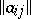 is invertible and, hence, defines an element of the group
is invertible and, hence, defines an element of the group 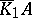 , denoted by
, denoted by 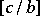 . If
. If 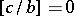 , the bases
, the bases 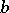 and
and  are said to be equivalent. It is clear that
are said to be equivalent. It is clear that
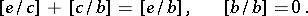 |
For any exact sequence 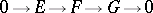 of free
of free 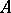 -modules and bases
-modules and bases  of
of 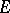 and
and 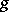 of
of  one can define a basis
one can define a basis  of
of 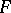 , where the images of the elements
, where the images of the elements  form the basis
form the basis 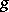 . The equivalence class of this basis depends only on those of
. The equivalence class of this basis depends only on those of  and
and 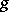 . Now let
. Now let
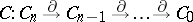 |
be a complex of free 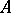 -modules
-modules 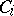 with chosen bases
with chosen bases 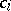 , whose homology complex is free, with a chosen basis
, whose homology complex is free, with a chosen basis  . Let the images of the homomorphisms
. Let the images of the homomorphisms 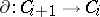 again be free, with basis
again be free, with basis 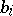 . The combinations
. The combinations 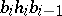 define a new basis in
define a new basis in 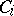 . Then the torsion of the complex
. Then the torsion of the complex 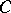 is given by the formula
is given by the formula
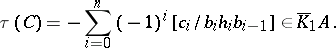 |
This torsion does not depend on the choice of the bases  for the boundary groups but only on
for the boundary groups but only on 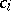 and
and  .
.
Given a pair 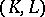 consisting of a finite connected complex
consisting of a finite connected complex 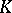 and a subcomplex
and a subcomplex 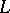 which is a deformation retract of
which is a deformation retract of 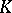 , one puts
, one puts 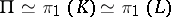 . If
. If 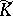 and
and 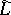 are the universal covering complexes for
are the universal covering complexes for 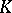 and
and 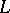 , then
, then  defines a chain mapping
defines a chain mapping 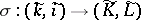 and hence a mapping of chain groups
and hence a mapping of chain groups 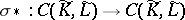 , i.e.
, i.e. 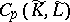 is a
is a  -module. One thus obtains a free chain complex
-module. One thus obtains a free chain complex
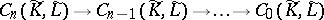 |
over 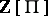 . The homology of this complex is trivial, i.e.
. The homology of this complex is trivial, i.e.  is a deformation retract of
is a deformation retract of 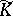 .
.
Let 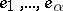 be
be 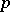 -chains in
-chains in 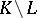 . For each chain
. For each chain 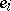 one chooses a representative
one chooses a representative 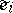 in
in 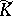 lying above
lying above 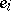 and fixes its orientation. Then
and fixes its orientation. Then 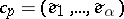 is a basis in
is a basis in 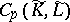 ; hence there is defined a subset
; hence there is defined a subset 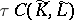 of
of  , called the torsion. In general it depends on the choice of the bases
, called the torsion. In general it depends on the choice of the bases 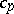 . However, the image of this set in the Whitehead group
. However, the image of this set in the Whitehead group 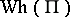 consists of a single element
consists of a single element 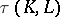 , called the Whitehead torsion of the pair
, called the Whitehead torsion of the pair  .
.
An important property of the Whitehead torsion is its combinatorial invariance. Whether  is a topological invariant is not known (1984).
is a topological invariant is not known (1984).
Let 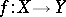 be a homotopy equivalence (
be a homotopy equivalence (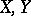 chain complexes). Then the torsion of the mapping
chain complexes). Then the torsion of the mapping 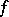 is defined as
is defined as  , where
, where 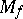 is the mapping cylinder of
is the mapping cylinder of  . If
. If 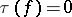 , then
, then 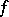 is called a simple homotopy equivalence. Properties of the torsion
is called a simple homotopy equivalence. Properties of the torsion 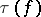 are: 1) if
are: 1) if  is an inclusion, then
is an inclusion, then  ; 2)
; 2) 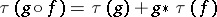 ; 3) if
; 3) if 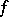 is homotopic to
is homotopic to 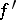 , then
, then 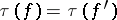 ; 4) if
; 4) if 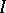 is the identity mapping of a simply-connected complex with Euler characteristic
is the identity mapping of a simply-connected complex with Euler characteristic 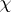 , then
, then 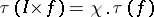 .
.
References
| [1] | J.H.C. Whitehead, "Simple homotopy types" Amer. Math. J. , 72 (1950) pp. 1–57 |
| [2] | J.W. Milnor, "Whitehead torsion" Bull. Amer. Math. Soc. , 72 (1966) pp. 358–426 |
Comments
The topological invariance of 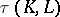 is treated in [a1]–[a3].
is treated in [a1]–[a3].
References
| [a1] | T.A. Chapman, "Topological invariance of Whitehead torsion" Amer. J. Math. , 96 (1974) pp. 488–497 |
| [a2] | S. Ferry, "The homeomorphism group of a compact Hilbert cube manifold is an ANR" Ann. of Math. , 106 (1977) pp. 101–119 |
| [a3] | J.E. West, "Mapping Hilbert cube manifolds to ANR's: a solution to a conjecture of Borsuk" Ann. of Math. , 106 (1977) pp. 1–18 |
Whitehead torsion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitehead_torsion&oldid=49211