Whitehead multiplication
A multiplication in homotopy groups 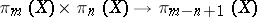 , defined by G.W. Whitehead . In
, defined by G.W. Whitehead . In 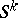 one takes a fixed decomposition into two cells
one takes a fixed decomposition into two cells 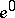 and
and 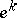 . Then the product of spheres
. Then the product of spheres 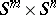 has a decomposition into cells
has a decomposition into cells 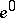 ,
, 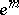 ,
, 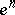 ,
, 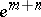 . Therefore the characteristic mapping
. Therefore the characteristic mapping 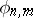 :
:
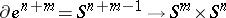 |
factorizes as
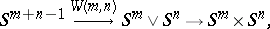 |
where 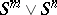 is a bouquet of spheres. Now, take classes
is a bouquet of spheres. Now, take classes 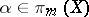 and
and 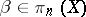 , represented by mappings
, represented by mappings 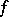 and
and 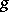 . Then the Whitehead product
. Then the Whitehead product 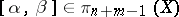 is given by the composition
is given by the composition
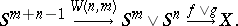 |
The following properties are satisfied by this product:
1) 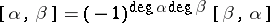 ;
;
2) if 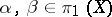 , then
, then 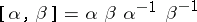 ;
;
3) if 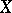 is
is  -simple, then
-simple, then 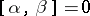 for
for 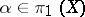 ,
, 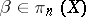 ;
;
4) if 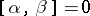 for all
for all 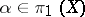 ,
, 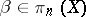 , then
, then 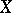 is
is  -simple;
-simple;
5) if 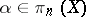 ,
, 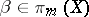 ,
, 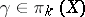 ,
,  , then
, then
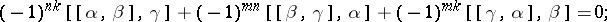 |
6) the element 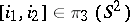 , where
, where 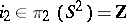 is a generator, is equal to twice the generator of
is a generator, is equal to twice the generator of 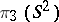 ;
;
7) the kernel of the epimorphism  is generated by one element,
is generated by one element, 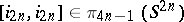 , where
, where 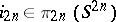 is the canonical generator.
is the canonical generator.
References
| [1a] | G.W. Whitehead, "On products in homotopy groups" Ann. of Math. , 47 (1946) pp. 460–475 |
| [1b] | G.W. Whitehead, "A generalization of the Hopf invariant" Ann. of Math. , 51 (1950) pp. 192–237 |
Comments
References
| [a1] | G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) |
| [a2] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. 419–420 |
| [a3] | S.-T. Hu, "Homotopy theory" , Acad. Press (1959) pp. 138–139 |
Whitehead multiplication. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitehead_multiplication&oldid=49209