Weyl connection

A torsion-free affine connection on a Riemannian space 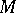which is a generalization of the Levi-Civita connection in the sense that the corresponding covariant differential of the metric tensor 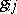of is not necessarily equal to zero, but is proportional to . If the affine connection on 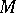is given by the matrix of local connection forms

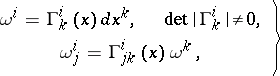(1)

and 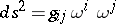, it will be a Weyl connection if and only if

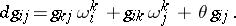(2)

Another, equivalent, form of this condition is:

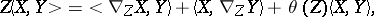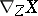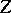where , the covariant derivative of with respect to , is defined by the formula

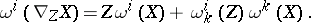With respect to a local field of orthonormal coordinates, where 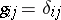, the following equation is valid:

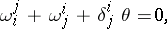i.e. any torsion-free affine connection whose holonomy group is the group of similitudes or one of its subgroups is a Weyl connection for some Riemannian metric on .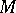

If in (1) 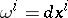, then for a Weyl connection

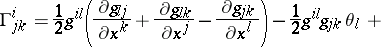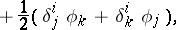where 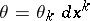. Since

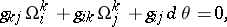the tensor

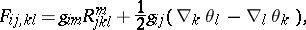called the directional curvature tensor by H. Weyl, is anti-symmetric with respect to both pairs of indices:

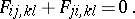Weyl connections were introduced by Weyl [1].

References

[1]	H. Weyl, "Reine Infinitesimalgeometrie" Math. Z. , 2 (1918) pp. 384–411
[2]	A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian)
[3]	G.B. Folland, "Weyl manifolds" J. Differential Geom. , 4 (1970) pp. 145–153