Weingarten derivational formulas
From Encyclopedia of Mathematics
Formulas yielding the expansion of the derivative of the unit normal vector to a surface in terms of the first derivatives of the position vector of this surface. Let  be the position vector of the surface, let
be the position vector of the surface, let 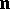 be the unit normal vector and let
be the unit normal vector and let 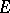 ,
,  ,
, 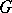 ,
, 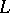 ,
,  ,
, 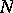 be the coefficients of the first and second fundamental forms of the surface, respectively; the Weingarten derivational formulas will then take the form
be the coefficients of the first and second fundamental forms of the surface, respectively; the Weingarten derivational formulas will then take the form
 |
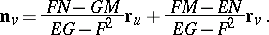 |
The formulas were established in 1861 by J. Weingarten.
References
| [1] | P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian) |
Comments
References
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
| [a2] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) |
How to Cite This Entry:
Weingarten derivational formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weingarten_derivational_formulas&oldid=49201
Weingarten derivational formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weingarten_derivational_formulas&oldid=49201
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article