Weil domain
From Encyclopedia of Mathematics
A special case of an analytic polyhedron. A bounded domain 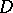 in
in  -dimensional space
-dimensional space 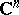 is said to be a Weil domain if there exist
is said to be a Weil domain if there exist 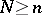 functions
functions 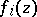 ,
, 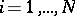 , holomorphic in a fixed neighbourhood
, holomorphic in a fixed neighbourhood  of the closure
of the closure 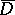 , such that
, such that
1) 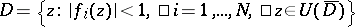 ;
;
2) the faces of the Weil domain 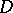 , i.e. the sets
, i.e. the sets
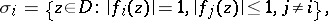 |
have dimension 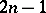 ;
;
3) the edges of the Weil domain 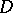 , i.e. the intersections of any
, i.e. the intersections of any 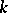 (
(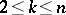 ) different faces, have dimension
) different faces, have dimension 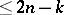 .
.
The totality of all  -dimensional edges of a Weil domain is called the skeleton of the domain. The Bergman–Weil representation applies to Weil domains. These domains are named for A. Weil [1], who obtained the first important results for these domains.
-dimensional edges of a Weil domain is called the skeleton of the domain. The Bergman–Weil representation applies to Weil domains. These domains are named for A. Weil [1], who obtained the first important results for these domains.
References
| [1] | A. Weil, "L'intégrale de Cauchy et les fonctions de plusieurs variables" Math. Ann. , 111 (1935) pp. 178–182 |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
| [3] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
Comments
References
| [a1] | B.A. Fuks, "Introduction to the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [a2] | G.M. [G.M. Khenkin] Henkin, J. Leiterer, "Theory of functions on complex manifolds" , Birkhäuser (1984) |
How to Cite This Entry:
Weil domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_domain&oldid=49200
Weil domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_domain&oldid=49200
This article was adapted from an original article by M. Shirinbekov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article