Web differentiation

A special concept in the differentiation of set functions 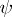. A web 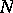is a totality of subdivisions 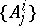of a basic space 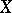with measure 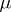such that

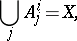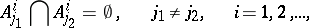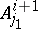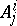and for each it is possible to find a set containing it. All are measurable, and their totality approximates in a certain sense, [1], all measurable sets. If 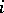is fixed, the sets 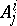are said to be sets of rank 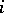. For each point 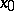and any there exists precisely one set 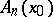of rank containing the point .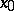

The expression

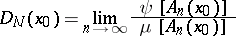is said to be the derivative of the function 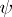along the web 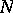at the point 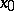, if that limit in fact exists. The concept of derived numbers along the web 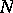can also be defined.

The simplest example of web differentiation is the differentiation of the increment of a function in one real variable by rational dyadic intervals of the form .

The web derivative of a countably-additive set function 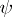exists almost everywhere and is identical with the density of the absolutely continuous component of 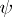. In an -dimensional space, web differentiation of semi-open intervals whose diameters tend to zero as their ranks increase [2] are usually studied.

The concepts of a web and of web differentiation may be generalized to the case of abstract spaces without a measure [3].

References

[1]	G.E. Shilov, B.L. Gurevich, "Integral, measure and derivative: a unified approach" , Dover (1977) (Translated from Russian)
[2]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)
[3]	H. Kenyon, A.P. Morse, "Web derivatives" Mem. Amer. Math. Soc. , 132 (1973)

Comments

In [1], "web differentiation" has been translated as "differentiation along a net" (Sect. 10.2). In it (Sect. 10.3), a generalization to Vitali systems is given.

The notion of web derivative for measures seems due to Ch.J. de la Vallée-Poussin [a1]. Nowadays it looks as a particular case of a theorem on convergence of martingales (cf. Martingale) and one of the best ways to prove the Radon–Nikodým theorem.

References

[a1]	Ch.J. de la Vallée-Poussin, "Intégrales de Lebesgue. Fonctions d'ensembles. Classe de Baire" , Gauthier-Villars (1936)