Weak solution
From Encyclopedia of Mathematics
of a differential equation
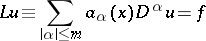 |
in a domain 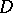
A locally integrable function  satisfying the equation
satisfying the equation
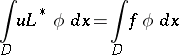 |
for all smooth functions 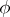 (say, of class
(say, of class  ) with compact support in
) with compact support in  . Here, the coefficients
. Here, the coefficients  in
in
are assumed to be sufficiently smooth and 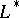 stands for the formal Lagrange adjoint of
stands for the formal Lagrange adjoint of 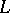 :
:
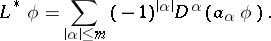 |
For example, the generalized derivative 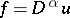 can be defined as the locally integrable function
can be defined as the locally integrable function 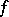 such that
such that  is a weak solution of the equation
is a weak solution of the equation 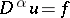 .
.
In considering weak solutions of , the following problem arises: under what conditions are they strong solutions (cf. Strong solution)? For example, in the case of elliptic equations, every weak solution is strong.
References
| [1] | A.V. Bitsadze, "Some classes of partial differential equations" , Gordon & Breach (1988) (Translated from Russian) |
Comments
References
| [a1] | S. Agmon, "Lectures on elliptic boundary value problems" , v. Nostrand (1965) |
| [a3] | D. Gilbarg, N.S. Trudinger, "Elliptic partial differential equations of second order" , Springer (1983) |
How to Cite This Entry:
Weak solution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_solution&oldid=49184
Weak solution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_solution&oldid=49184
This article was adapted from an original article by A.P. Soldatov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article