Weak relative minimum
A minimal value 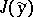 attained by a functional
attained by a functional 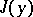 on a curve
on a curve 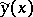 ,
, 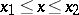 , such that
, such that 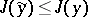 for all comparison curves
for all comparison curves 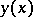 satisfying the first-order
satisfying the first-order  -proximity condition
-proximity condition
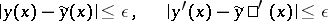 | (1) |
throughout the interval 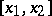 . It is assumed that the curves
. It is assumed that the curves 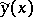 ,
, 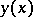 satisfy the given boundary conditions.
satisfy the given boundary conditions.
If in (1) one disregards the  -proximity condition on the derivative, then this leads to the zero-order
-proximity condition on the derivative, then this leads to the zero-order  -proximity condition. The minimal value of the functional
-proximity condition. The minimal value of the functional 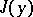 in a zero-order
in a zero-order  -neighbourhood is called a strong relative minimum.
-neighbourhood is called a strong relative minimum.
Since the zero-order  -proximity condition distinguishes a wider class of curves than the first-order
-proximity condition distinguishes a wider class of curves than the first-order  -proximity condition, every strong relative minimum is also a weak relative minimum, but not conversely.
-proximity condition, every strong relative minimum is also a weak relative minimum, but not conversely.
For an extremal 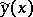 to give a weak relative minimum, the Legendre condition must hold on it. For a strong relative minimum, the more general Weierstrass conditions (for a variational extremum) must hold. In terms of optimal control theory, the distinction between these necessary conditions means that for a weak (strong) relative minimum, it is necessary that, at the points of the extremal, the Hamilton function have a local maximum (absolute maximum) with respect to the control (in agreement with the Pontryagin maximum principle).
to give a weak relative minimum, the Legendre condition must hold on it. For a strong relative minimum, the more general Weierstrass conditions (for a variational extremum) must hold. In terms of optimal control theory, the distinction between these necessary conditions means that for a weak (strong) relative minimum, it is necessary that, at the points of the extremal, the Hamilton function have a local maximum (absolute maximum) with respect to the control (in agreement with the Pontryagin maximum principle).
Sufficient conditions for a weak relative minimum impose certain requirements only on the extremal 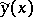 , whereas in the case of a strong minimum, one requires conditions similar in the sense to hold not only on
, whereas in the case of a strong minimum, one requires conditions similar in the sense to hold not only on 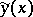 , but also in a certain zero-order
, but also in a certain zero-order  -neighbourhood of it. An extremal will be a weak relative minimum if the strong Legendre and strong Jacobi conditions hold along it. An extremal will be a strong relative minimum if it can be imbedded in a field of extremals at all points of which the Weierstrass function is non-negative.
-neighbourhood of it. An extremal will be a weak relative minimum if the strong Legendre and strong Jacobi conditions hold along it. An extremal will be a strong relative minimum if it can be imbedded in a field of extremals at all points of which the Weierstrass function is non-negative.
References
| [1] | M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian) |
| [2] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
Comments
References
| [a1] | D.G. Luenberger, "Optimization by vector space methods" , Wiley (1969) |
| [a2] | L. Cesari, "Optimization - Theory and applications" , Springer (1983) |
Weak relative minimum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_relative_minimum&oldid=49182