Weak extremum

A minimal or maximal value 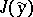, attained by a functional 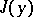on a curve 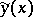, , 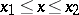for which one of the following inequalities holds:

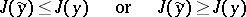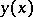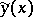for all comparison curves situated in an -proximity neighbourhood of with respect to both 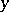and its derivative:

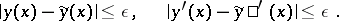The curves 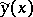, 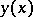must satisfy the prescribed boundary conditions.

Since the maximization of is equivalent to the minimization of 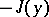, one often speaks of a weak minimum instead of a weak extremum. The term "weak" emphasizes the fact that the comparison curves 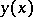satisfy the -proximity condition not only on the ordinate but also on its derivative (in contrast to the case of a strong extremum, where the -proximity of 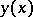and 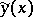refer only to the former).

By definition, a weak minimum is a weak relative minimum, since the latter gives a minimum among the members of a subset of the whole class of admissible comparison curves for which 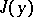makes sense. However, for the sake of brevity, the term "weak minimum" is used for both.

References

[1]	M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian)
[2]	V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian)