Wallis formula
From Encyclopedia of Mathematics
A formula which expresses the number  as an infinite product:
as an infinite product:
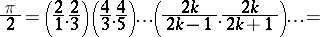 | (1) |
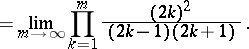 |
There exist other variants of this formula, e.g.:
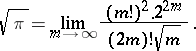 | (2) |
Formula (1) was first employed by J. Wallis [1] in his calculation of the area of a disc; it is one of the earliest examples of an infinite product.
References
| [1] | J. Wallis, "Arithmetica infinitorum" , Oxford (1656) |
Comments
Formula (1) is a direct consequence of Euler's product formula
 |
with 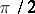 .
.
It can also be obtained by expressing 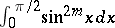 and
and 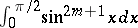 in terms of
in terms of 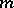 , and by showing that
, and by showing that
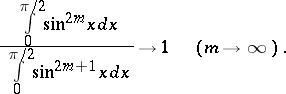 |
Formula (2) can be derived from (1) by multiplying the numerator and the denominator of 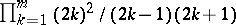 by
by  .
.
References
| [a1] | T.M. Apostol, "Calculus" , 2 , Blaisdell (1964) |
| [a2] | C.H. Edwards jr., "The historical development of the calculus" , Springer (1979) |
| [a3] | P. Lax, S. Burstein, A. Lax, "Calculus with applications and computing" , 1 , Springer (1976) |
| [a4] | D.J. Struik (ed.) , A source book in mathematics: 1200–1800 , Harvard Univ. Press (1986) |
How to Cite This Entry:
Wallis formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wallis_formula&oldid=49169
Wallis formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wallis_formula&oldid=49169
This article was adapted from an original article by T.Yu. Popova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article