Vladimirov variational principle

A variational principle for the stationary single-velocity homogeneous transport equation (cf. Transport equations, numerical methods)

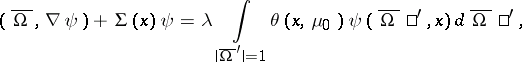(1)

with boundary condition

(2)

where is the boundary of a convex bounded domain . If the scatter indicatrix is an even function of , transition to the new unknown function

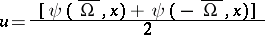reduces the problem (1), (2) to self-adjoint form. In the problem thus obtained, Vladimirov's variational principle for the smallest eigenvalue states that is the minimum of the functional

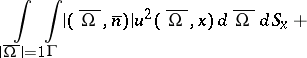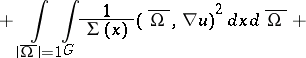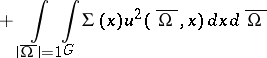on the set of functions which satisfy the condition

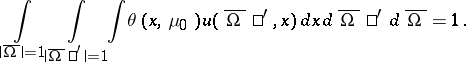The corresponding (non-negative) eigenfunction realizes the minimum of the functional [3]. In this variational principle the respective boundary conditions are natural. Variational principles for higher eigenvalues and for the non-homogeneous problem are formulated in a similar manner.

The principle was first obtained by V.S. Vladimirov [1], and it yielded the optimum boundary conditions in the method of spherical harmonics (cf. Spherical harmonics, method of). Vladimirov's variational principle, in conjunction with finite difference methods, is extensively employed in numerical computations of neutron physics.

References

[1]	V.S. Vladimirov, "Mathematical problems in the theory of single-velocity particle transfer" , Moscow (1961) (In Russian)
[2]	G.I. Marchuk, "Methods of calculation of nuclear reactors" , Moscow (1961) (In Russian)
[3]	B. Davison, "Neutron transport theory" , Oxford Univ. Press (1957)

Comments

Cf. also Vladimirov method.