Virial decomposition
virial series
The series on the right-hand side of the equation of state of a gas:
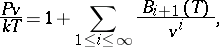 |
where  is the pressure,
is the pressure,  is the temperature,
is the temperature,  is the specific volume, and
is the specific volume, and  is the Boltzmann constant. The term of the series which contains the
is the Boltzmann constant. The term of the series which contains the  -th virial coefficient
-th virial coefficient  describes the deviation of the gas from ideal behaviour due to the interaction in groups of
describes the deviation of the gas from ideal behaviour due to the interaction in groups of  molecules.
molecules.  can be expressed in terms of irreducible repeated integrals
can be expressed in terms of irreducible repeated integrals 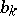 :
:
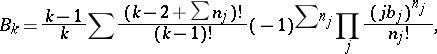 |
summed over all natural numbers  ,
,  , subject to the condition
, subject to the condition
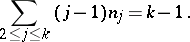 |
In particular,
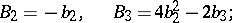 |
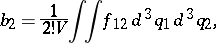 |
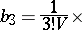 |
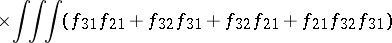 |
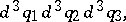 |
where
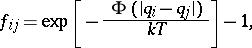 |
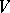 is the volume of the gas, the integration extends over the total volume occupied by the gas, and
is the volume of the gas, the integration extends over the total volume occupied by the gas, and  is the interaction potential. There is a rule for writing down
is the interaction potential. There is a rule for writing down  for any
for any  in terms of
in terms of 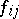 . The expression obtained after simplification is:
. The expression obtained after simplification is:
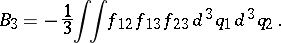 |
In practice, only the first few virial coefficients can be calculated.
Power series in  , with coefficients expressed in terms of
, with coefficients expressed in terms of  , can be used to represent equilibrium correlation functions for
, can be used to represent equilibrium correlation functions for  particles; a corollary of this fact is that the equation of state can be obtained in a simple manner [3].
particles; a corollary of this fact is that the equation of state can be obtained in a simple manner [3].
There exists a quantum-mechanical analogue of the virial decomposition.
References
| [1] | J.E. Mayer, M. Goeppert-Mayer, "Statistical mechanics" , Wiley (1940) |
| [2] | R. Feynman, "Statistical mechanics" , M.I.T. (1972) |
| [3] | N.N. Bogolyubov, "Problems of a dynamical theory in statistical physics" , North-Holland (1962) (Translated from Russian) |
| [4] | G.E. Uhlenbeck, G.V. Ford, "Lectures in statistical mechanics" , Amer. Math. Soc. (1963) |
Virial decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Virial_decomposition&oldid=49149