Vinogradov hypotheses

Several hypotheses on central problems in analytic number theory, advanced by I.M. Vinogradov [1], [2] at various times.

Hypotheses on the distribution of power residues and non-residues.

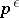One of the oldest and best known such hypotheses is that the distance between neighbouring quadratic non-residues is a magnitude of order . (Cf. Power residue; Quadratic residue.)

Hypotheses on estimates of trigonometric sums.

One of them is that

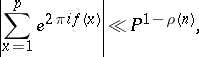where

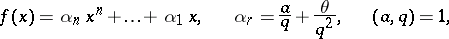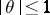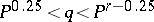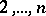, , is one of the numbers , and 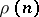has the order 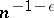. (Cf. Trigonometric sums, method of; Vinogradov method.)

Hypotheses on the number of solutions of Diophantine equations.

One such hypothesis states that the number of solutions of the system of equations

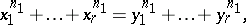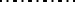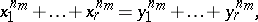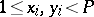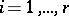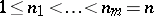, , , where is constant, will be a magnitude of order 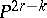, , 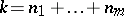for all , where has order 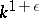. (Cf. Diophantine equations.)

Hypotheses on the number of integer points in domains in the plane and in space.

One such hypothesis states that the number of integer points in the sphere 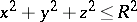can be expressed by the formula

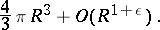(Cf. Integral points, distribution of.)

References

[1]	I.M. Vinogradov, "Some problems in analytic number theory" , Proc. 3-rd All-Union Mat. Congress (Moscow, 1956) , 3 , Moscow (1958) pp. 3–13 (In Russian)
[2]	I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian)
[3]	I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian)