Verbal subgroup

The subgroup of a group generated by all possible values of all words (cf. Word) of some set , when run through the entire group independently of each other. A verbal subgroup is normal; the congruence defined on the group by a verbal subgroup is a verbal congruence (see also Algebraic systems, variety of).

Examples of verbal subgroups: 1) the commutator subgroup 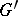of a group defined by the word 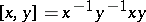; 2) the -th commutator subgroup 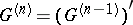; 3) the terms of the lower central series

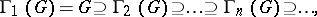where is the verbal subgroup defined by the commutator

4) the power subgroup 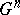of the group defined by the words .

The equality 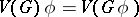is valid for any homomorphism 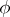. In particular, every verbal subgroup is a fully-characteristic subgroup in . The converse is true for free groups, but not in general: The intersection of two verbal subgroups may not be a verbal subgroup.

Verbal subgroups of the free group of countable rank are especially important. They constitute a (modular) sublattice of the lattice of all its subgroups. Verbal subgroups are "monotone" : If 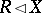, 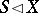(here 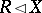means that 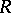is a normal subgroup of ) and , then .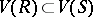

References

[1]	A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian)
[2]	H. Neumann, "Varieties of groups" , Springer (1967)