Vekua method

in the theory of infinitesimal deformations

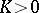A method which can be applied to the case when certain quantities which characterize the deformation of surfaces with positive Gaussian curvature are, in a conjugate-isothermal parametrization, generalized analytic functions (cf. Generalized analytic function). This makes it possible to reduce the study of the deformation of surfaces with variable to a definite problem concerning surfaces with 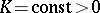, whose infinitesimal deformations (cf. Infinitesimal deformation) are described by ordinary analytic functions, thus establishing a far-reaching analogy between the properties of deformations of surfaces with variable and constant positive Gaussian curvature.

References

[1]	I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian)