Vector field, source of a
From Encyclopedia of Mathematics
A point of the vector field 
with the property that the flow of the field through any sufficiently small closed surface 
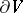enclosing it is independent of the surface and positive. The flow
 |
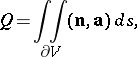where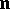 
is the outward unit normal to 
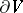and 
is the area element of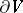 
, is called the power of the source. If 
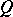is negative, one speaks of a sink. If the sources are continuously distributed over the domain 
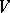considered, then the limit
 |
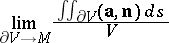is called the density (intensity) of the source at the point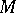 
. It is equal to the divergence of 
at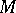 
.
Comments
A combination of a source and a vortex in a hydrodynamical flow gives rise to a swirl flow.
References
| [a1] | J. Marsden, A. Weinstein, "Calculus" , 3 , Springer (1988) |
| [a2] | H. Triebel, "Analysis and mathematical physics" , Reidel (1986) pp. Sect. 16 |
How to Cite This Entry:
Vector field, source of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_field,_source_of_a&oldid=49137
Vector field, source of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_field,_source_of_a&oldid=49137
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article